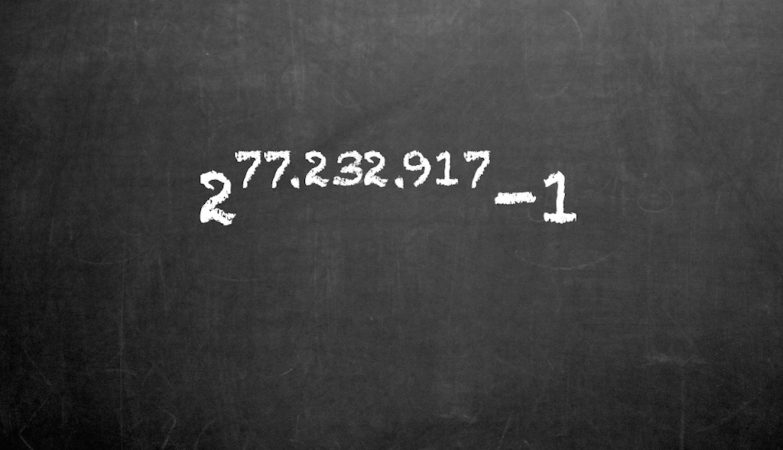23,249,425 são os dígitos que compõem o recentemente descoberto número primo. Chama-se M77232917 e é o 50.º número primo deste tipo a ser descoberto.
Chama-se primo Mersenne (como o padre matemático francês Marin Mersenne) e é o resultado da multiplicação de dois juntos muitas vezes e subtraindo um ao número final. O M77232917 foi descoberto ao calcular dois elevado a 77,232,917, subtraindo um.
Este é quase um milhão de dígitos maior do que o anterior número primo, também um primo Mersenne. E torna-o demasiado longo para que possamos escrevê-lo aqui para si.
Conforme os números vão ficando maiores, os números primos – um número divisível por 1 e pelo próprio – tornam-se cada vez mais difíceis de encontrar. Tornam-se cada vez mais distantes e não há qualquer padrão da sua distribuição, por isso não é possível usar um algoritmo que os descubra.
Até a formula para encontrar números primos Mersenne não é um método infalível, é apenas a redução aos números mais prováveis.
Por isso, depois de usar uma fórmula para criar o número, o cientista tem depois que passar pelo difícil processo de o testar, dividindo por todos os números que possam ser um fator de divisão. Quanto maior o número, mais tempo é necessário.
Alguns softwares podem ser usados para procurar primos Mersenne e testá-lo, o que aconteceu com o M77232917.
Como parte do Great Internet Mersenne Prime Search (GIMPS), o voluntário Jonathan Pace, um engenheiro elétrico com 51 anos do Tennessee, nos EUA, fez a descoberta com software especializado no seu PC. Desde os 14 que o engenheiro tenta descobrir um número primo e esta é a primeira vez que consegue.
O número já foi descoberto a 26 de dezembro de 2017, mas provar que era primo demorou seis dias de computação sem parar. Depois disso, quatro diferentes programas de software a operar em quatro configurações diferentes de hardware para verificar a descoberta.
O anterior recorde de um número primo Mersenne foi descoberto em janeiro de 2016, com menos 910,807 dígitos do que o recente M77232917.
O novo recorde é tão grande que teriam que ser impressas nove mil páginas ou 118 quilómetros – um pouco mais do que a distância entre Lisboa e Santarém (104 quilómetros) – com dois dígitos por cada centímetro.
Porquê procurar por números primos? O M77232917 é demasiado grande para servir o seu propósito, mas a criptografia usa grandes números primos apenas porque são difíceis de descobrir. Combine dois números primos como chave de criptografia e terá algo muito mais difícil de quebrar – e, conforme os computadores vão ficando mais poderosos, os números primos têm de ser maiores para acompanhar o ritmo.
Este números podem também ajudar-nos a compreender os números em si. Se descobrirmos primos suficientes, talvez um dia seja possível fazer a descoberta de um padrão.
Mas para os matemáticos, tanto amadores como profissionais, os números primos grandes tornaram-se algo como uma caça ao tesouro – quase literalmente agora que o GIMPS oferece prémios monetários para novos recordes.
Pace vai receber três mil dólares (3,370 euros) pela sua descoberta.
Se, como o Pace, também quiser descobrir um número primo, mesmo que isso leve o resto da sua vida a fazer, pode fazer o download do software aqui e ler as instruções aqui.
ZAP // Science Alert