Uma nova pesquisa descobriu o princípio matemático que torna os desenhos de árvores tão facilmente reconhecíveis, mesmo em obras de arte abstrata.
Um estudo inovador publicado na PNAS Nexus revelou que a nossa capacidade de reconhecer árvores em obras de arte – independentemente do estilo ou da cultura – está ligada a um princípio matemático fundamental conhecido como o expoente de escala do diâmetro dos ramos.
Esta descoberta sugere que mesmo as representações abstratas de árvores mantêm a sua forma reconhecível devido a um padrão universal encontrado na natureza.
Realizado por investigadores da Universidade de Michigan e da Universidade do Novo México, o estudo examinou a forma como a espessura dos ramos das árvores influencia a nossa perceção da sua natureza arbórea. A investigação baseia-se em observações feitas por artistas como Leonardo da Vinci, mas aplica uma análise matemática moderna para compreender o fenómeno em maior profundidade.
“Há algumas caraterísticas da arte que são estéticas ou subjetivas, mas podemos usar a matemática para as descrever”, afirmou o autor principal, Jingyi Gao.
O seu estudo centrou-se na geometria fratal, um conceito matemático em que os padrões se repetem em diferentes escalas. Nas árvores, isto manifesta-se através de estruturas ramificadas que se replicam de forma auto-similar.
Os investigadores analisaram especificamente o expoente de escala do diâmetro dos ramos, que descreve a forma como a espessura dos ramos muda à medida que as árvores se dividem em secções mais pequenas, refere o SciTech Daily.
Jingyi Gao e Mitchell Newberry
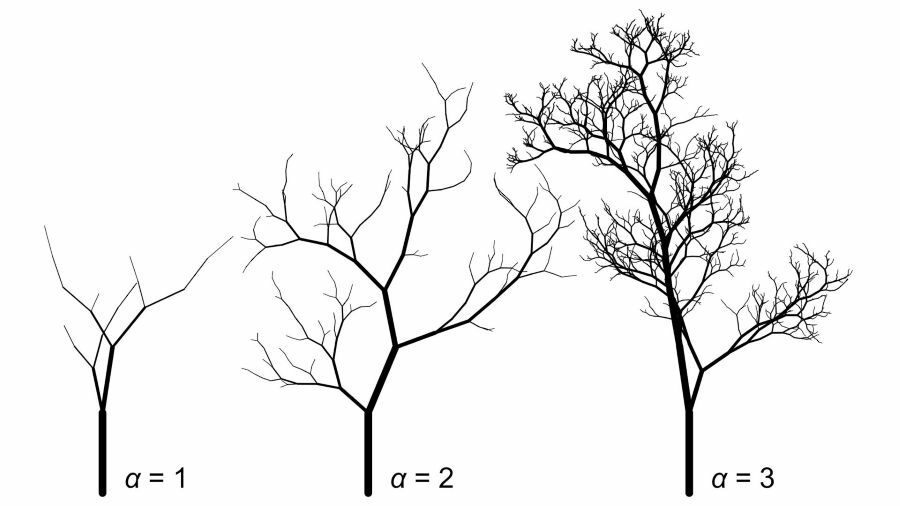
Estas imagens geradas por computador mostram como a alteração do expoente de escala do diâmetro do ramo – indicado pela letra grega alfa – de uma “árvore” altera a sua aparência. Os investigadores mostraram que árvores reais e objetos reconhecíveis como árvores na arte têm um alfa entre 1,5 e 3.
Ao examinar as representações de árvores em várias obras de arte – incluindo esculturas em pedra indianas do século XVI, uma pintura japonesa do século XVIII e obras modernistas holandesas do início do século XX – a equipa descobriu que os artistas preservavam instintivamente este princípio matemático.
Mesmo em representações altamente estilizadas, as árvores mantiveram a sua forma reconhecível quando o expoente de escala correspondia a valores naturais, normalmente entre 1,5 e 3.
Um exemplo notável é o do pintor holandês Piet Mondrian. Na sua obra de 1911, De grijze boom (A árvore cinzenta), Mondrian utilizou apenas linhas pretas sobre um fundo cinzento, mas a árvore manteve-se imediatamente reconhecível. Os investigadores descobriram que o expoente de escala dos ramos estava dentro do intervalo das árvores reais.
No entanto, na sua obra posterior de 1912, Bloeiende appelboom (Macieira em flor), em que a escala foi alterada, a árvore tornou-se menos distinguível, com os desenhos a abrir a porta a várias interpretações, como dançarinos, escamas de peixe ou padrões abstratos.
O estudo destaca a forma como os princípios matemáticos sustentam a expressão artística, reforçando a ideia de que as estruturas inerentes à natureza moldam a perceção humana.
















