A Internet está dividida e em busca da resposta certa para uma equação matemática. Pode a mesma equação ter dois resultados distintos?
No dia 28 de julho, um utilizador lançou a confusão no Twitter: Quanto é 8÷2(2+2)?
Os utilizadores tentaram resolver a equação matemática, mais de 13 mil vezes até. Mas se uns dizem que é óbvio que a resposta é 1, outros dizem que é impossível que o resultado seja outro que não 16.
Ainda assim, segundo o Observador, todos concordam numa coisa: a primeira operação a resolver é a que está entre parêntesis, 2+2, ou seja 4. O problema vem a seguir: perante 8÷2(4) que operação deve ser feita primeiro? A divisão ou a multiplicação? A equação surge numa imagem do filme The Last Naruto: the movie.
Nos Estados Unidos, as respostas distintas têm a ver com o método com que cada um aprendeu a fazer operações matemáticas na escola: o PEMBDAS (Parenthesis, Exponents, Multiplication, Division, Addition, Subtraction) ou o BODMAS (Brackets, Orders, Division, Multiplication, Addition, Subtraction).
As mnemónicas servem para ajudar a memorizar a forma como uma equação deve ser resolvida. No PEMBDAS, a multiplicação aparece antes da divisão, enquanto que no BODMAS, é a divisão que aparece primeiro.
Desta forma, quando a conta é feita dando prioridade à multiplicação, perante 8÷2(4), multiplica-se primeiro 2 por 4, o que dá 8. E ficamos com 8÷8=1. Mas se a prioridade for dada à divisão, perante 8÷2(4), divide-se primeiro 8 por 2, o que dá 4 – e ficamos com 4(4), uma multiplicação, que dá 16.
Contudo, isto não significa que a equação possa ter dois resultados diferentes. Manda a Matemática que a multiplicação e a divisão têm igual precedência (tal como a soma e a subtração) e, desde que não haja parêntesis envolvidos, as operações devem ser resolvidas da esquerda para a direita.
Isto significa que, neste caso concreto, a divisão deve realizar-se primeiro, tal como explica Presh Talwalkar, autor de vários sobre jogos matemáticos, num vídeo no YouTube.
O especialista, que estudou Economia e Matemática em Stanford, nos Estados Unidos, explica que esta é a única conclusão possível segundo os métodos modernos de cálculo. Ainda assim, ressalva que houve alturas na História em que os métodos antigos poderiam conduzir ao resultado de 1.

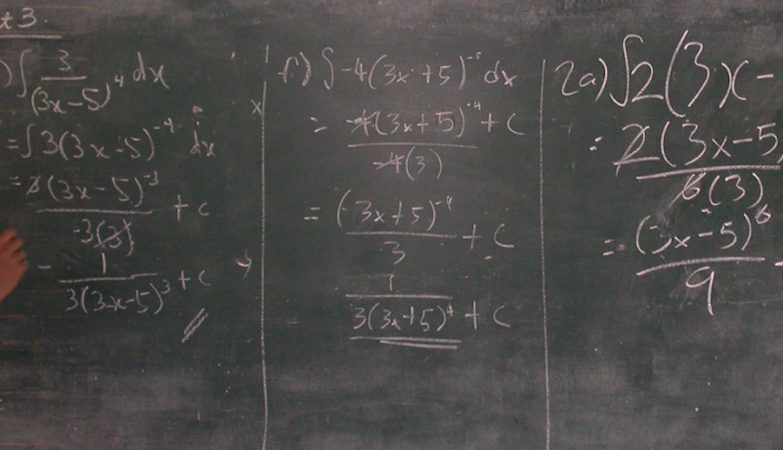












Resolvendo 2+2, elimina-se os parenteses.
só se elimina os parênteses se tiver sinal antes deles, o que não é o caso dessa equação.
A questão é tb uma fração.
8/2(2+2) = 8:8 = 1.
Como questão linear:
8:2(2+2)
8:(2*2+2*2)=
8:(4+4)=
8:8=1.
Ao ser acrescentado manualmente o sinal de “.”
entre o 8:2.(2+2)= a notação foi fraudada de 2 para 3 termos, o 2 que era multiplicador do conteúdo do parenteses, passou a ser divisor do 8, o que gerou um acréscimo de 16 vezes no resultado correto que é 1.
Ressalto que o 2(2+2) é um termo implícito, equivalente a 8, individualmente, ou quando presente em qualquer expressão.
8:2(2+2)=2(2+2):8=8/8=1
A solução do Parenteses só se efetiva após multiplicar o conteúdo pelo 2 externo, que é seu principal componente.
v. Link…
https://www.khanacademy.org/math/pre-algebra/pre-algebra-arith-prop/pre-algebra-ditributive-property/a/distributive-property-explained
Tem apenas um resultado que é igual a 16. Entre os parênteses tem um operação, que é de multiplicação.
Errado! Não se pode operar com um número associado a outros entre parêntesis sem primeiro resolver as contas com estes. 2.(2+2) é uma totalidade que não pode ser separada para operar com outra.
O resultado e 16 pois 4×4=16
Há uma única resolução existem e correta. Resultado é 1. E posso provar com dados matemáticos corretos e bem convincentes. Ninguém iria descordar, nem mesmo o melhor matemático de todos os tempos.
Que dó..
É… ninguém vai discordar que tu não percebes nada de matemática!…
Bem… Parece que o Eu! também não…
Rafael,
O prejuízo causado por essas expressões de proveta vem sendo muito grande em termos de confusão no raciocínio das pessoas. É alarmante a quantidade de variantes dessas notações e o desleixo desses aventureiros com relação à Matemática. A inserção do operador “.”, a omissao da distributiva, a mudança de 2 para 3 termos, a inversão da função do 2( , e a menção ao PEMDAS como regra matemática , demonstra que esse pessoal não tem escrúpulos rumo ao interesse próprio.
Triste, pessoas se posicionam como se fossem donas do conhecimento absoluto, não aceitam o contraditório, baseados em regras preliminares, sem profundidade nenhuma, se acham o dono do saber, coitados!
Oliver,
Não fique triste.
De minha parte mantenho minha afirmação de que trata-se de uma trama fraudulenta. A questão é básica 8:2(2+2). Qualquer calculadora resolve 2(2+2)=8.
8:8=1.
Você nao acha estranho dividir 8 por ele mesmo e achar 16, como é possivel 8 resultar 8×16=128?
Tem milagre aí no meio!
Não sou Senhor do Mundo, mas isto é conta para fazer nos dedos.
Aí tem uma multiplicação implícita: 2(2+2)=8, o 2 externo multiplica o conteúdo do parenteses, só após o parenteses está resolvido. É a regra da distributiva, não viu o link da khanacademy.org?
Repito, comeca uma expressão de 2 termos, tb fracionária, 8:2(2+2)=1, 8/2(2+2); 8 numerador e 2(2+2) denominador =8/8= 1 .
E a inserção do “.” altera para 3 termos, 8:2.(2+2)=16, ou seja frauda à original, ainda invertendo a função do 2 de multiplicador do parenteses, para divisor do 8, causando uma majoração de 16 vezes no resultado.
Matemática é exata, isto aí é como 1+1=2.
Coitados! É,, dos omissos, aqueles que afirmaram que a eliminação do parenteses, sem aplicar a multiplicação pelo 2, e que ainda inseriram o “.” o e garantiram que não alterava nada.
Mentiram, fraudaram a questão.
Sabe: A matemática não tem diferentes interpretações. 2+2 é igual a 4. Isso não está sujeito a diferentes ideias de como fazer a “conta”. Na matemática ou é ou não é! Também, ao contrário do “expert” Presh Talwalkar, a matemática não muda de acordo com o tempo. 2+2 era igual a 4 em 1917 assim como em 2021! A matemática não é ambígua a menos que haja variaveis envolvidas e, mesmo assim, os resultados serão quase sempre previsiveis. Bem… Será que em 3021 2+2 será igual x?
Concordo plenamente com voce. Faca a prova substituindo um valor por x como uma expressão numérica. 8: 2( x+ 2) = 1 e vera que o resultado e verdadeiro.
Boa Elisabete! Excelente exemplo! Talvez o grande “expert” Presh Talwalkar devesse ver isto. E é um exemplo que era válido em 1917 assim como nos nossos dias!
“desde que não haja parêntesis envolvidos, as operações devem ser resolvidas da esquerda para a direita.”
Mas há parênteses envolvidos ué
Ele(a) quis dizer você deve resolver primeiro os parênteses e depois você retira eles da equação. Aí você pode resolver da esquerda pra direita.
Se esta equação fosse apresentada na forma de fração não haveria qualquer dúvida.
Admitindo a equação enquanto fração temos de admitir que esta equação não seria igual a 8 no numerador e 2(2+2) no denominador. Seria 8 no numerador, no denominador seria 2 e então o resultado da divisão seria multiplicado por (2+2). Logo o resultado só pode mesmo ser o 16.
…confesso que também respondi 1, o que é obviamente errado, mas para isso a restante equação depois do sinal de divisão deveria estar entre parentesis também.
Resumindo:
8/2×4 =16
8/(2×4) =1
Penso que o que mais confunde na equação apresentada é a prioridade da operação entre parentesis sugerir a resolução da equação a partir dela para a esquerda.
Por outro lado em engenharia raramente se usa o sinal de divisão desta forma, mas sim em forma de fracção que automaticamente delimita os dois operandos a dividir, na falta da barra fracção automaticamente visualizamos a barra naquele ponto a separar toda a equação.
Mas é interessante, sem dúvida.
Oliver,
Não fique triste.
De minha parte mantenho minha afirmação de que trata-se de uma trama fraudulenta. A questão é básica 8:2(2+2). Qualquer calculadora resolve 2(2+2)=8.
8:8=1.
Você nao acha estranho dividir 8 por ele mesmo e achar 16, como é possivel 8 resultar 8×16=128?
Tem milagre aí no meio!
Não sou Senhor do Mundo, mas isto é conta para fazer nos dedos.
Aí tem uma multiplicação implícita: 2(2+2)=8, o 2 externo multiplica o conteúdo do parenteses, só após o parenteses está resolvido. É a regra da distributiva, não viu o link da khanacademy.org?
Repito, comeca uma expressão de 2 termos, tb fracionária, 8:2(2+2)=1, 8/2(2+2); 8 numerador e 2(2+2) denominador =8/8= 1 .
E a inserção do “.” altera para 3 termos, 8:2.(2+2)=16, ou seja frauda à original, ainda invertendo a função do 2 de multiplicador do parenteses, para divisor do 8, causando uma majoração de 16 vezes no resultado.
Matemática é exata, isto aí é como 1+1=2.
Coitados! É,, dos omissos, aqueles que afirmaram que a eliminação do parenteses, sem aplicar a multiplicação pelo 2, e que ainda inseriram o “.” o e garantiram que não alterava nada.
Mentiram, fraudaram a questão.
“confesso que também respondi 1, o que é obviamente errado”. Óbviamente? Não me parece. A matemática não é mutável, independentemente da forma como é apresentada. 2+3 é igual a cinco assim como 3+2 também. O Edson tem razão. A soma e multiplicação não podem ser deixadas para último. Não é possivel divvidir o 8 por um algarismo ainda não fotmado. Tenho de o descodificar primeiro
(2 x (2+2) = 2 X 4 = 8) para poder dividi-lo por 8!
…deveria ter visualizado o video antes de comentar, diz basicamente o mesmo.
Só pergunto aos amáveis solucionadores e aos redactores da notícia, afinal “onde é que está a equação?”.
É favor relembrar a definição de equação…
Cara Pantufa,
A equação está formulada na questão “Quanto é 8÷2(2+2)?”
Se preferir a formulação estrita de uma equação, aqui fica: 8÷2(2+2)=X
“Quanto é 8÷2(2+2)?” significa “Qual o resultado da expressão numérica 8÷2(2+2)?”
Não há qualquer equação.
Olá, segundo eu me lembro: 8:2(2+2) = 8/2 +4 = 32/2= 16
[ 1º) o que está dentro do parêntese =4; 2º) a multiplicação =8X4=32; 3º) a divisão =32:2=16]
Ó Manuela… Olhe que dá 16 mas não é assim que se fazem as contas. Isso está tudo errado.
Primeiro 8:2 = 4
depois (2+2) = 4
e 4×4 =16
Como diria o falecido Álvaro Cunhal: “Olhe que não, olhe que não”. o 2(2+2) deve ser reolvido antes de fazer a divisão porque está ligado pela multiplicação. Só depois de multiplicar 2 pela soma é que se pode dividir. Eu aprendi na escola também (há muito tempo) e não me parece que as regras tenham mudado. Não é possível dar dois resultados! Só este: 8÷2(2+2) = 8÷2(4) = 8÷8 = 1
Bem… Segundo o “expert” (da treta!) Presh Talwalkar, fazia-se antigamente como descrevi, mas da maneira “moderna” é ao contrário. Hmmmm…. Quer dizer que a matemática que só tem um resultado (por é assim precisa) afinal tem outro porque é mais moderno? Pior! Há gente (infelizmente eu incluido) que andam a perder tempo com isto em vez de pensar em coisas bem mais importantes como explicar ás pessoas o que é DISTANCIAMENTO SOCIAL!!!
A segunda resposta é minha fiz sem regra foi de cabeça!
A 1ª resposta pedi ajuda ao meu primo! colei do facebook! Grande confusão!! Que trapalhada! ha!ha!ha!
Tem toda a razão.
Sempre vi essa conta como o 8 sendo o dividendo e o 2(2+2) como o divisor devido a falta do sinal de vezes, e com isso daria 1 já que:
8
———- = 1
2(2+2)
Mas como colocado na matéria ficaria:
8
— * (2+2)
2
Temos dois resultados diferentes, para diferentes equações:
16 para 8:2(2+2)
1 para 8:(2(2+2))
No entanto não pode deixar de se considerar como resultado possível 1 para a primeira equação.
Coisas da matemática.
Como aprendi na escola, (há muito tempo) quando temos um algarismo ao lado do parênteses como é o caso, a equação deve-se ler exatamente como descreve “8:(2(2+2))”. O 2 está intrinsecamente ligado á soma por isso não pode haver uma divisão antes de se resolver a segunda parte da equação, (ou outra operação matemática) ou seja, é necessário fazer-se a adição dentro do parênteses, depois a multiplicação do 2 pelo resultado da adição anterior e, só depois se pode fazer a divisão. essa treta de que antigamente se fazia assim mas agora faz-se de outro modo, não pega! A matemática é uma ciência exata. Não é mutável ao saber das modas… Honestamente não entendo a dúvida aqui… Acho que é para ocupar pessoas como eu que não têm nada para fazer… Desculpe o desabafo.
No meu modo de ver o termo equação é mais diverso em seu significado, sendo uma questão ou assunto que precisa ser equacionado em qualquer área do cotidiano, seja na Matemática, seja na politica, na Saúde, enfim em qualquer setor. Um exemplo claro a equação da pandemia…
Considero mais relevante do que certo ou errado o uso do termo para a expressão 8:2(2+2), o fato de as pessoas terem dificuldades em resolver esta divisão de proveta, articulada por espertos para gerarem controvérsia na WEB e ganharem alguns níqueis com o tráfego de dados que artificialmente produzem.
A gênese desse cálculo tem como embrião a divisão de um número por ele mesmo, decomposto por n formas possíveis.
No caso 8:8, uma divisão ou fração de 8, dividendo ou numerador por 2(2+2) que é 8 também, como divisor ou denominador, como poderia ser 4(1+1), 2(1+3), e muitas outras variantes que no conjunto representassem oito. Combinando sob diversas formas entre submúltiplos ou múltiplos do valor decomposto.
É até 8:16(0,25+0,25)=1.
E se fosse o contrário? 2(2+2):8=1 é óbvio.
Seria a prova que 2(2+2):8=8:2(2+2)= 8/8=1.
Fizeram o mesmo com 6:6, 20:20 e muitas outras estultices, que além do resultado instantâneo, facílimo e cristalino, apresentam uma segunda incógnita: o que pretendem fazer com a Matemática aqueles que estão a gerar essas premissas disfarçadas de modernismo? Fúteis, artificiais, fantasiadas de verdade, chanceladas por algumas pessoas “graduadas” como
legítima expressão do moderno, consumindo espaços valiosos na vida real e conectada das pessoas, recebendo lastro de autenticidade de gigantes da tecnologia, através de videos egoístas eivados de vícios e farsas. Fraudes e personalismo.
Mentirosos, quanto mais se recua no tempo mais se percebe que os métodos, forma e expressão eram mais qualificados e perfeitos e foram sendo banalizados à medida que se avançou na tecnologia, era para ser o contrário.
Quem quiser conferir o resultado de 8:2(2+2)=1, 6:2(2+1)=1, 20:2(5+5)=1, poderia acessar as calculadoras SOLVER de:
chegg com
Solver Math Microsoft.com
solumaths.com e
Wolframalpha.com
Precisávamos como racionais equacionar a
Imensa controvérsia injustificada gerada por essa fração de numerador oito e denominador 2(2+2)=8.
Boa tarde! Simples,assim.8÷2(2+2)=4×4=16 ou 4-4=0 ou 4+2+2=8 ou 4÷4=1 ou 8÷6=1,030303….ou,ñ se chega a nada,complexa,heim,kkk.Vai ,ai,uma mnemônica para ñ esquecer à regrinha de se resolver às equaçōes(MUDAS)=multiplicação,divisão,adição e subtração .”As equaçōes estão MUDAS”
Boa tarde! Simples,assim.8÷2(2+2)=4×4=16 ou 4-4=0 ou 4+2+2=8 ou 4÷4=1 ou 8÷6=1,030303….fora às outras q já foram citadas; ñ se chega a nada,complexa,heim,kkk.Vai ,ai,uma mnemônica para ñ esquecer à regrinha para resolver equaçōes(MUDAS)=multiplicação,divisão,adição e subtração .”As equaçōes estão MUDAS”
Sempre me disseram que a Matemática é uma ciência exata.
Agora tenho muitas dúvidas !
Boa tarde! Precisamente!!!
Encontrar aqui alguém que concorda comigo… fez-me ganhar o dia!!!! Já me ri tanto com isto! Mas tanto…. ahahahahahahahaha
Obrigada pela resposta.
Isto é demais….”
Pois é… É preciso vir um “expert” da treta dizer-te que aquilo que aprendeste agora já não é assim. Que a matemática era uma ciência extata em 1917 e agora é “outra” ciência exata. Treta!
8:2x(2+2)
Primeiro deve se resolver a conta dentro dos parênteses
8:2*4
Se sabe que x:y=x*1/y
Ou seja, um número dividido por outro é igual a multiplicar seu inverso
Isso prova que a conta que se deve fazer é 8:2 e não 2×4
Logo
4×4=16
(8÷2)(2+2) = 4×4 = 16
8÷(2(2+2)) = 8÷(2×4) = 8÷8 = 1
Qual é a dúvida? É só colocar na calculadora científica. O resultado é 16. O que confirma que a prioridade é da esquerda para a direita. Se os computadores e calculadoras fizessem cálculos errados muitas obras de engenharia já teriam colapsado.
Entenda, ordem de equações… Multiplicação e divisão primeiro, soma e subtração segundo, ok, mas daí quando existem parenteses ele são primeiro então… Veja.
8/2(2+2)= 8/2(4)= olhe o parêntese…
8/8= 1. Só tem como ser 16 se fizer errado.
Não viaja, a resposta é 16, quando você soma o (2+2) você “elimina” o parêntese.
Não há mais operação dentro de parêntese, sendo Assim, resolve-se da esquerda para a direita.
É 16!
Errado estás tu, e com tantas explicações, já nem sequer tens desculpa para escrever esses disparates!…
Pois… E parece que não é o único.
Pra resolve tem que umsar o metodo da distributiva 8÷2(2+2)
Resolucao distributiva
2(2+2)=4+4=8
8÷8=1
Não se deve usar o lemnisco (÷) para representar um divisão.
Ver ISO 80000-2 e o problema fica resolvido.
Gente, pelo amor de Jah, né. Pela regra matemática, a divisão é feita antes da multiplicação. Mentira que fizeram tantos mil cálculos. Qualquer pessoa que realmente estudou matemática sabe disso.
Depende onde estudou.
Pois…
Para mim digam o que disserem uma divisão é um quociente, logo 8/2x(2+2)=1. O facto de o denominador ser o lado há direita da sinal de divisão constitui um parêntesis implícito. Logo a ambiguidade é que a expressão para dar 16 devia ser: (8/2)(2+2)=16 … Isto vem da interferência de um conceito de escrita matemática inglês que se espalhou na Ásia e nos é devolvido no cálculo escrito em binário nos chips dos computadores.
Pimba! Na mouche, Jorge, na mouche!
Bolas! É óbvio que dá 16! Não sei onde vão buscar o 8:(2(2+2))! Ao não haver o parênteses que escrevi atrás tem que se fazer 8/2 e o resultado multiplica por 4!
A expressão escrita daquela forma é:
8
— x (2+2)
2
e é claro como a água!
Boa tarde
Se usarmos a prioridade da multiplicação e divisão e e a propriedade distributiva da multiplicação ficamos com
a/b*(c+d) = a/b*c +a/b*d
Ou seja
8/2 *2 + 8/2*2 =16
Então pense desta forma, por favor. 8 a dividir por um algarismo que é o resultado de 2x(2+2). Já reparou como o 2+2 está intrinsecamente ligado ao 2? Então fará sentido retirá-lo da sua “ligação” resultando num resultado absolutamete diferente? A lei da prioridade tem de ser usada, concerteza, mas neste caso nem sequer se põe essa questão. é 8 a dividir por um elgarimso que, por acaso é também 8 (tudo por causa do parêntesis precedido do 2.
segundo o Observador, todos concordam numa coisa: a primeira operação a resolver é a que está entre parêntesis, 2+2, ou seja 4. E usar a propriedade da distributiva da multiplicação em relação à adição nao?
Sim!
Distributiva.
8:2(2+2)=
8:(2*2+2*2)=
8:(4+4)=
8:8=1
v. Link…
https://www.khanacademy.org/math/pre-algebra/pre-algebra-arith-prop/pre-algebra-ditributive-property/a/distributive-property-explained
1. Fazem-se as operações entre parênteses.
2. Potências.
3. Multiplicação/Divisão, da esquerda para a direita, independentemente da ordem das mesmas.
4. Adição/Subtracção, da esquerda para a direita, independentemente da ordem das mesmas.
Logo, 8 ÷ 2 (2 + 2) = 8 ÷ 2 * 4 = 4 * 4 = 16
Nota: Assim que se efectua o primeiro cálculo, entre parênteses, retiram-se estes, i.e. (2 + 2) = 4.
Para além disso gostava de saber de onde vem o termo “equação”? É uma expressão, as equações necessitam de incógnitas, explicitamente dadas para efectuar o cálculo.
Parabéns!!..
Ainda ninguém tinha chegado a essa conclusão!…
.
Se gostavas de saber de onde vem o termo equação, lias tudo com atenção!…
“A equação está formulada na questão “Quanto é 8÷2(2+2)?”
Se preferir a formulação estrita de uma equação, aqui fica: 8÷2(2+2)=X”
8/2(2+2)=?
2(2+2) = (4+4)
8/(4+4) = 8/8 = 1
8/2(2+2)=?
2(2+2) = 2^3
8/2^3 = 8/8 = 1
Bem… próximo passo: tentares completar o Ensino Básico!
Não te armes, badameco!
Essa necessidade crónica de atenção é sintoma de que não estás muito bem…
É… Parece-me que padece do mesmo problema.
Ele respondeu a um comentário meu de Agosto de 2019 e tu, andas aqui a fazer o quê?!
É… Respondendo a “Ele respondeu a um comentário meu de Agosto de 2019 e tu, andas aqui a fazer o quê?!”… Pergunto-lhe o mesmo: “e tu, andas aqui a fazer o quê?!”
Tu és mesmo muito lerdo e ainda és mais lerdo porque provavelmente desconfiando que o és ainda tiveste coragem de vir aqui disparatar. É obra…
8/2(2+2) =
8/2*(2+2) =
8/2*4 =
4*4 =
16
Sim!
Distributiva.
8:2(2+2)=
8:(2*2+2*2)=
8:(4+4)=
8:8=1
v. Link…
https://www.khanacademy.org/math/pre-algebra/pre-algebra-arith-prop/pre-algebra-ditributive-property/a/distributive-property-explained
O transito tem regras, a matemática também,
1º Resolver o que está dentro de parênteses (2+2)=4 ficamos com 8:2(4) ou 8:2×4
2º As operaçãoes x e : têm a mesma prioridade por isso resolve-se a que aparece em 1.º lugar. 8:2=4.
3.º falta 4×4=16.
As regras são assim definidas poderiam ser outras, mas quem se estendia?
De acordo com o que está escrito na operação o resultado é 16. Se a operação foi escrita dessa forma o resultado só poderá dar 16.
A questão é tb uma fração.
8/2(2+2) = 8:8 = 1.
Como questão linear:
8:2(2+2)
8:(2*2+2*2)=
8:(4+4)=
8:8=1.
Ao ser acrescentado manualmente o sinal de “.”
entre o 8:2.(2+2)= a notação foi fraudada de 2 para 3 termos, o 2 que era multiplicador do conteúdo do parenteses, passou a ser divisor do 8, o que gerou um acréscimo de 16 vezes no resultado correto que é 1.
Ressalto que o 2(2+2) é um termo implícito, equivalente a 8, individualmente, ou quando presente em qualquer expressão.
8:2(2+2)=2(2+2):8=8/8=1
A solução do Parenteses só se efetiva após multiplicar o conteúdo pelo 2 externo, que é seu principal componente.
v. Link…
https://www.khanacademy.org/math/pre-algebra/pre-algebra-arith-prop/pre-algebra-ditributive-property/a/distributive-property-explained
Acho que o ruimvp já deu a resposta. Se os computadores e calculadoras cientificas já foram programados com a forma de efetuar os cálculos, então não há mais dúvidas.
…..suponho que estás “avarias” matemáticas, talvez ajudem a explicar os milhoes desaparecidos nomeadamente em bancos……e que a maioria das pessoas aprenderam da escola, as quatro operações aritméticas existentes, contas de somar, contas de subtrair, contas de dividir e contas de multiplicar…………no entanto houve quem aprendesse mais uma operação aritmética…
as contas de SUMIR !!
Em relação a solução de 8/2(2+2), eu acredito fortemente que depende se a questão se refere a uma questão de Aritmética (Escola primária) ou Álgebra (Escola Secundária). Pela omissão (proposital) do sinal da multiplicação antes do parênteses, vou ficar com o modelo mais sofisticado da Álgebra, caso contrário, quem “bolou” a questão teria colocado o sinal da multiplicação. No caso, se estivesse visualizando uma expressão: 8/2x, e se eu te dissesse que x=4, você provavelmente diria que o resultado é 1. Na Álgebra quando se omite uma multiplicação, ela é geralmente referente a omissão do . (ponto), e na Álgebra, o . tem precedência sobre a multiplicação ou divisão (apesar de ser referente a uma multiplicação). Obviamente, na questão que gerou dúvida, não foi um esquecimento do sinal da multiplicação, foi uma omissão proposital, típica da Álgebra, e neste caso, ela TEM SIM precedência sobre uma multiplicação entre números. Portanto, o resultado seria igual a 1. Após este raciocínio vou ainda dar um “plus” a mais que enfatiza esse resultado. Na questão proposta e que gerou controvérsia na internet, existe um espaço entre o 8 e o sinal da divisão e outro espaço entre o sinal da divisão e o primeiro 2. Mas não existem espaços entre o 2 e o parênteses, ou seja, no caso da Álgebra, seria algo sem dúvidas: 8 / 2x
sendo x = (2 + 2)
Resultado = 1
Simples assim. Sem dúvidas.
Pelo exposto, a questão é de Álgebra. Se fosse Aritmética (o que obviamente não é), aí sim, seriam 16 a resposta.
No meu entender, as pessoas estão a analisar isto de um forma errada. Passo a explicar o porquê:
Quando pomos algo como c(a+b) estamos a priorizar a multiplicação do c ao resultado da soma de a e b.
Existe uma diferença em pormos c x (a+b) ou c(a+b). E a grande confusão reside neste detalhe. À primeira vista parece igual, ou inofensivo passar de c x (a+b) para c(a+b). Mas não o é.
Qdo o pomos c(a+b) estamos a priorizar essa operação em relação às demais que possam existir, ou seja é o mesmo que estamos a colocar: (c x (a+b)).
Se tivéssemos:
8 % 2 x (2+2) a conta é:
16
Ao termos:
8 % 2(2+2) equivale a 8%(2x(2+2))
E isso é igual a 1.
Outro exemplo que possam analisar é:
8%2a. Agora substituam o a por 4.
8/2a não é igual a 8/(2a).
8/2a = 8/2xa enquanto 8/(2a) = 8/(2xa).
Exatamente, manuais de engenharia ensinam exatamente isso a/bc é equivalente à a/(b*c). Sendo a multiplicação efetuada antes da divisão!
8/2(2+2)=X
=4(2+2)
=8+8
X=16
Certo assim!!
É só seguir o PEMDAS.
O que ficaria assim:
8÷2(2+2)=8÷2×4=4×4=16.
Depois de fazer o que está dentro de parêntesis. Vamos fazer a conta de esquerda para a direita. Daí chegamos ao resultado correto.
8:2(2+2) é expressão de 2 termos em que 8 é dividendo ou numerador e 2(2+2) que é oito decomposto, divisor ou denominador, eis que tb é uma fracionária 8/8=1. Não percebem os adeptos do outro cálculo que ao adicionar operador “.”entre 8:2.(5+5), alteram completamente a notação original, que passa a operação para 3 termos e desloca o 2 de multiplicador do conteúdo do parenteses para divisor do dividendo, majorando o resultado em 16 vezes. A notação 8:2(2+2)=1,
limpa, cristalina, perfeita; a notação fraudada, 8:2.4 é outra expressão com resultado bem distinto (16).
2(2+2)=8 em qualquer calculadora e 2(2+2):8=1 e. 2(2+2).2=16.
O problema viral é uma fraude, como milhares de outros semelhantes na WEB, começou cisne e se transformou em peru.
Lamentável o nível dos professores “youtubers” que para faturar pontos estão ludibriando milhões de alunos pelo mundo afora.
Um golpe medíocre que demonstra o despreparo de nossa gente em Matemática.
Felizmente existe uma parcela da população que tem forte conhecimento na área para desmascarar os “espertos”.
Eu os desafio a derrubar meus argumentos, nesta e em todas as expressões adulteradas.
Acrescento que não foi aplicada a propriedade distributiva que é regra matemática:
8:2(2+2)=
8:(2*2+2*2)=
8:(4+4)=
8:8=1
V. Link
https://www.khanacademy.org/math/pre-algebra/pre-algebra-arith-prop/pre-algebra-ditributive-property/a/distributive-property-explained
Como algumas pessoas escrevem aqui, (como o Edson e o Rodrigo) isso estaria correto se a equação fosse 8 : 2 x (2 + 2). Mas não é! O 2(2+2) é um só algarismo (a ser calculado) que será dividido; neste caso, por 8!
Na mosca!
Convicção é o que precisamos!
1 sem qualquer dúvida!
O Pedro, apesar de estar debaixo da ponte, tem melhor poder de observação. De facto segundo o que eu aprendi, não se trata de uma equação é uma simples expressão numérica e parece-me que, por isso, o título deveria ser alterado para não induzir em erro.
8:2(2+2) é expressão de 2 termos em que 8 é dividendo ou numerador e 2(2+2) que é oito decomposto, divisor ou denominador, eis que tb é uma fracionária 8/8=1. Não percebem os adeptos do outro cálculo que ao adicionar operador “.”entre 8:2.(5+5), alteram completamente a notação original, que passa a operação para 3 termos e desloca o 2 de multiplicador do conteúdo do parenteses para divisor do dividendo, majorando o resultado em 16 vezes. A notação 8:2(2+2)=1,
limpa, cristalina, perfeita; a notação fraudada, 8:2.4 é outra expressão com resultado bem distinto (16).
2(2+2)=8 em qualquer calculadora e 2(2-2):8=1 e. 2(2+2).2=16.
O problema viral é uma fraude, como milhares de outros semelhantes na WEB, começou cisne e se transformou em peru.
Lamentável o nível dos professores “youtubers” que para faturar pontos estão ludibriando milhões de alunos pelo mundo afora.
Um golpe medíocre que demonstra o despreparo de nossa gente em Matemática.
Felizmente existe uma parcela da população que tem forte conhecimento na área para desmascarar os “espertos”.
Eu os desafio a derrubar meus argumentos, nesta e em todas as expressões adulteradas.
Infelizmente o MEC é bem omisso na questão.
Embora não tenho um “forte conhecimento na área” concordo em absoluto consigo (no que diz respeito á equação e não ao resto porque não tenho dados para ter uma opinião). Isto parece-me apenas uma tentativa de fazer as pessoas perder tempo (como eu) a dar atenção a uma coisa que não tem (não deveria) importância. A única conclusão que chego é que há muita confusão na cabeça das pessoas e que as aulas de matemática, ou não foram bem dadas ou não foram compreendidas… Ou as duas coisas. Ou… Afinal a matemática já não é uma ciência exata. Talvez o 2+2 já não seja assim tão simples como isso…
Esta parte básica é fundamental para o aprendizado regular das etapas futuras da Matemática. O que se precisa é acabar com essa confusão que é uma realidade admitida pelos próprios instrutores..
O seu comentário aguarda validação
8:2(2+2) é expressão de 2 termos em que 8 é dividendo ou numerador e 2(2+2) que é oito decomposto, divisor ou denominador, eis que tb é uma fracionária 8/8=1. Não percebem os adeptos do outro cálculo que ao adicionar operador “.”entre 8:2.(5+5), alteram completamente a notação original, que passa a operação para 3 termos e desloca o 2 de multiplicador do conteúdo do parenteses para divisor do dividendo, majorando o resultado em 16 vezes. A notação 8:2(2+2)=1,
limpa, cristalina, perfeita; a notação fraudada, 8:2.4 é outra expressão com resultado bem distinto (16).
2(2+2)=8 em qualquer calculadora e 2(2+2):8=1 e 2(2+2).2=16.
O problema viral é uma fraude, como milhares de outros semelhantes na WEB, começou cisne e se transformou em peru.
Lamentável o nível dos professores “youtubers” que para faturar pontos estão ludibriando milhões de alunos pelo mundo afora.
Um golpe medíocre que demonstra o despreparo de nossa gente em Matemática.
Felizmente existe uma parcela da população que tem forte conhecimento na área para desmascarar os “espertos”.
Eu os desafio a derrubar meus argumentos, nesta e em todas as expressões adulteradas.
Infelizmente o MEC é bem omisso na questão.
Por gentileza na minha primeira remessa cometi um erro de escrita “2(2-2)” é 2(2+2), por isso reenviei o comentário corrigido.
Tenho em uso 8 calculadoras no celular que efetuam o cálculo corretamente. É 1.
Imagine que você vai doar 8 moedas para 2 grupos de
(2+2) pessoas, caberá uma moeda por pessoa, jamais 16 moedas per capita.
Toda a falha resulta da não aplicação da distributiva e defraudação da notação original.
A multiplicação do conteúdo do parenteses pelo 2 que o antecede é obrigatória, vide o link:
https://www.khanacademy.org/math/pre-algebra/pre-algebra-arith-prop/pre-algebra-ditributive-property/a/distributive-property-explained
A resposta é 1.
2(2+2)= (2×2) + (2×2)= 4+4= 8
Considerando o 8 antes do sinal de divisão: 8 a dividir por 8 é 1.
Confesso que não tinha pensado assim (que burrice!) mas é verdade! Já li respostas bem eloquentes e bem fundamentadas, mas a sua foi sintética e na mouche! Acho que o “expert” do Presh Talwalkar é tão “expert” que não consegue “ver” algo tão simples como o que escreveu. Acho que a inteligência acaba por atrapalhar. Quanto ao resto do pessoal… Há claramente uma grande confusão! Espero que esse pessoal nunca tenha depender da matemática para sobreviver. Não me parece que vão durar muito…
Edson Flores, E se você der 2 moedas a cada pessoa de cada grupo são (8 grupos X duas moedas) ou 2(4X2); seja 2 vezes 4 pessoas de cada grupo com 2 moedas cada)! isto é igual 8:2(2+2) = ou seja 8+8 =16
Repare não é (8:1) é (8:2) só que o 2 serve de multiplicador ao que está dentro do parêntese e o 8 soma-se com o resultado que está a seguir!
Eu baseei-me nas suas moedas, você estava a ir bem, só que se baralhou com o (8) que só serve para atrapalhar se nos distrairmos! É natural não se preocupe!
No meu modo de ver o termo equação é mais diverso em seu significado, sendo uma questão ou assunto que precisa ser equacionado em qualquer área do cotidiano, seja na Matemática, seja na politica, na Saúde, enfim em qualquer setor. Um exemplo claro a equação da pandemia…
Considero mais relevante do que certo ou errado o uso do termo para a expressão 8:2(2+2), o fato de as pessoas terem dificuldades em resolver esta divisão de proveta, articulada por espertos para gerarem controvérsia na WEB e ganharem alguns níqueis com o tráfego de dados que artificialmente produzem.
A gênese desse cálculo tem como embrião a divisão de um número por ele mesmo, decomposto por n formas possíveis.
No caso 8:8, uma divisão ou fração de 8, dividendo ou numerador por 2(2+2) que é 8 também, como divisor ou denominador, como poderia ser 4(1+1), 2(1+3), e muitas outras variantes que no conjunto representassem oito. Combinando sob diversas formas entre submúltiplos ou múltiplos do valor decomposto.
É até 8:16(0,25+0,25)=1.
E se fosse o contrário? 2(2+2):8=1 é óbvio.
Seria a prova que 2(2+2):8=8:2(2+2)= 8/8=1.
Fizeram o mesmo com 6:6, 20:20 e muitas outras estultices, que além do resultado instantâneo, facílimo e cristalino, apresentam uma segunda incógnita: o que pretendem fazer com a Matemática aqueles que estão a gerar essas premissas disfarçadas de modernismo? Fúteis, artificiais, fantasiadas de verdade, chanceladas por algumas pessoas “graduadas” como
legítima expressão do moderno, consumindo espaços valiosos na vida real e conectada das pessoas, recebendo lastro de autenticidade de gigantes da tecnologia, através de videos egoístas eivados de vícios e farsas. Fraudes e personalismo.
Mentirosos, quanto mais se recua no tempo mais se percebe que os métodos, forma e expressão eram mais qualificados e perfeitos e foram sendo banalizados à medida que se avançou na tecnologia, era para ser o contrário.
Quem quiser conferir o resultado de 8:2(2+2)=1, 6:2(2+1)=1, 20:2(5+5)=1, poderia acessar as calculadoras SOLVER de:
chegg com
Solver Math Microsoft.com
solumaths.com e
Wolframalpha.com
Precisávamos como racionais equacionar a
Imensa controvérsia injustificada gerada por essa fração de numerador oito e denominador 2(2+2)=8.
Sara,
a questão é que a quantidade de moedas é 8, dividendo. 2 é o numero de grupos de pessoas e 2+2 o numero de pessoas de cada grupo.
8 moedas : 2 grupos de (2+2) pessoas, ou seja 8:2(2+2)= 1.
O produto disponível para dividir limita-se a 8 moedas, 2 grupos está vinculado a (2+2) pessoas, no total 8 individuos, 8:8= 1 moeda por pessoa.
Esta é a notação em discussão 8:2(2+2)=8:8=1, mas tem a irmã quase gêmea 8:2*(2+2)=8:2*4=4*4=16 esta sim, apresenta o sinal de multiplicação antes do parenteses, é constituída de 3 termos, tendo alterada a função do 2 de multiplicador do conteúdo do parenteses para divisor do dividendo e que nao serve para o exemplo da divisão das moedas pois divide e multiplica elementos diferentes aí sim
8 :2 * 4 = 4 *4 = 16..
Sara,
Como eu gostaria de estar errado e ceder para a outra opinião. Aí ficaria aliviado.
Mas é impossível, estou certo, convicto,
este cálculo é de resultado 1. Há uma manipulação no sentido de fazer prevalecer o contrário.
Existe a notação: 8:2(2+2)=1 e existe a outra 8:2*(2+2)= 16.
O que fizeram para confundir, gerar controvérsia e tráfego na WEB, através de videos, foi iniciar o cálculo da original = 1 e, ao longo da explicação, alterá-la para a notação 8:2*(2+2), cujo resultado realmente é 16.
Esta fraude está confundindo muita gente, e, iguais a esta, proliferam centenas de variantes em expressiva parte do planeta.
A confusão é incalculável e muita cortina de fumaça é utilizada para ludibriar a verdade.
Trama planejada, treta desleal e inaceitável.
Era, é, e sempre será 2(2+2)=8 e
8:8=2(2+2):8= 8:2(2+2)=8:(2*2+2*2)=1.
O comentário atribuído ao sr Presh foi muito nebuloso.
… isto ainda se discute? Já percebi que não é nada óbvio ao contrário do que disse antes, aqui vão os meus cinco tostões (ou 0,0005€)
Então, discute-se e aparentemente vai continuar a ser discutido enquanto não se normalizarem muito melhor as notações matemáticas.
Apesar de ser repetido muitas vezes, a matemática não é tão universal como se diz, basta pensar nos diferentes métodos de ensino e nos sistemas métricos e imperial que tantos problemas reais dão, e este problema não é mais que uma provocação de alguém que percebeu uma falha nessa “universalidade”.
É preciso normalizar que quando se representa a notação 2(a+b) sem ponto ou sinal de multiplicação, o algarismo (nesta caso o 2) deve ser operado apenas ao valor no interior do parentesis e com a mesma prioridade deste, utilizando ou não a propriedade distributiva.
Mas se quisermos adicionar um ponto ou sinal de multiplicação, aí tem de ser representado como (2x(a+b)) ou (2.(a+b)) para manter a mesma função, caso contrário o operador pode perder a relação prioritária com o valor entre parentesis.
Este é o cerne de toda esta discussão, a falta de normalização, ou seja se a notação:
8%2(4) (sem qualquer ponto ou sinal)
é igual a
8%2×4 (=16)
ou a
8%(2×4) (=1)
e isto já sem entrar na necessidade de se usar o formato em fracção que simplificaria tudo.
O problema não está nas continhas que todos (uns melhor que outros) sabemos fazer, mas sim no que está subentendido a um operador que precede um parentesis sem qualquer sinal, se é apenas um multiplicador ao conteúdo deste, subentendendo um segundo parentesis, ou apenas mais um elemento da equação.
Enquanto não se normalizar isto, tendo a multiplicação e a divisão a mesma prioridade e não se usando o formato fraccionário, as operações são resolvidas da esquerda para a direita e o resultado correcto é 16 mas eu iria (e vou) sempre responder 1, pois parto do princípio que o operador do parentesis tem sempre prioridade, mesmo correndo o risco de estar errado, mas quase de certeza chegando ao resultado certo de acordo com quem escreveu a equação (e sim, já sei que aquilo não é uma equação).
Pensa você muito bem! A questão é fracionária e não se pode fugir disso, o seu resultado 8:2(2+2)=1, é 1, e não é petulância ou falta de humildade minha, é a verdade que Descartes conceitua como a busca que se está sempre a perseguir.
É uma divisão de 8 por ele mesmo decomposto ou “esquartejado” e qualquer n:n=1, é sempre foi, e sempre será. uma fração, uma divisão, com resultado 1.
Se como fração o resultado é 1,obrigatoriamente, como cálculo em linha será o mesmo. 8: 2(2+2) = 1.
Os que criaram essa “polêmica” esqueceram que a Matemática desmente o que fazem mal com ela, 8:2(2+2)=2(2+2):8=8/8=1.
PEMDAS, BODMAS, BIDMAS, GEMDAS tudo isso é bilhete, lembrança de memória, artificio para facilitar, que mal instruídos geraram esta confusão babélica injustificável.
Diversos apps gratuitos disponíveis na internet, calculam estas expressões e muito mais com exatidão, cito CALC 10, CALC BUSINESS, CALC 84, CALCES, CALCULATOR, HYPER SCIENTIFIC CALCULATOR, MATH SOLVER MICROSOFT, MATHEMATICS, PANECAL, MATHWAY… Também os SOLVER dos sites CHEGG.COM, SOLUMATHS.COM e WOLFRAMALPHA.COM disponibilizam o resultado de forma muito rápida e muito mais educação.
Testando em um deles o cálculo de 3 dessas expressões ao mesmo tempo encontra-se o mesmo resultado 1, pois 1*1*1=1:
8:2(2+2)*6:2(1+2)*20:2(5+5)=1, demonstrando que as 3 tem resultado 1.
O único cuidado que se deve ter é configurar os apps para considerar o cálculo implícito como a regra na configuração.
O cerne desta discussão resume-se em INTERPRETAÇÃO, pura e simples. Senão vejamos: em uma notação matemática a multiplicação será representada por “x” ou “.” ok? Então a expressão em voga poderia ser 2x(2+2) ou 2.(2+2). O que não está se considerando é que a supressão do sinal “.” na grafia não significa que ele deixou de existir, que não esteja lá! É o mesmo caso de não se representar números inteiros por 1,0 e sim 1 simplesmente. Então ao se escrever 2(2+2) é o mesmo que 2.(2+2). Não existe esta de que se trata de um número único a ser calculado e que portanto esta multiplicação teria precedência, etc,etc,etc… Fosse assim, então a representação correta seria (2(2+2)) e aí sim, teríamos um número “exclusivo” a ser calculado tendo a multiplicação prioridade em virtude dos parênteses que a envolvem. Assim, a expressão 8 ÷ 2(2+2) 8÷2.(2+2). Deve-se resolver o conteúdo dos parênteses e depois a sequência de operações na ordem em que aparecem da esquerda para a direita: 8÷2.(4)=> 4.4=16. Outro resultado diferente só seria possível se a expressão inicial fosse 8÷(2(2+2)), qdo teríamos:
8÷(2(4))=> 8÷ (2.4)=> 8÷8=1.
Espero ter colaborado.