ZAP
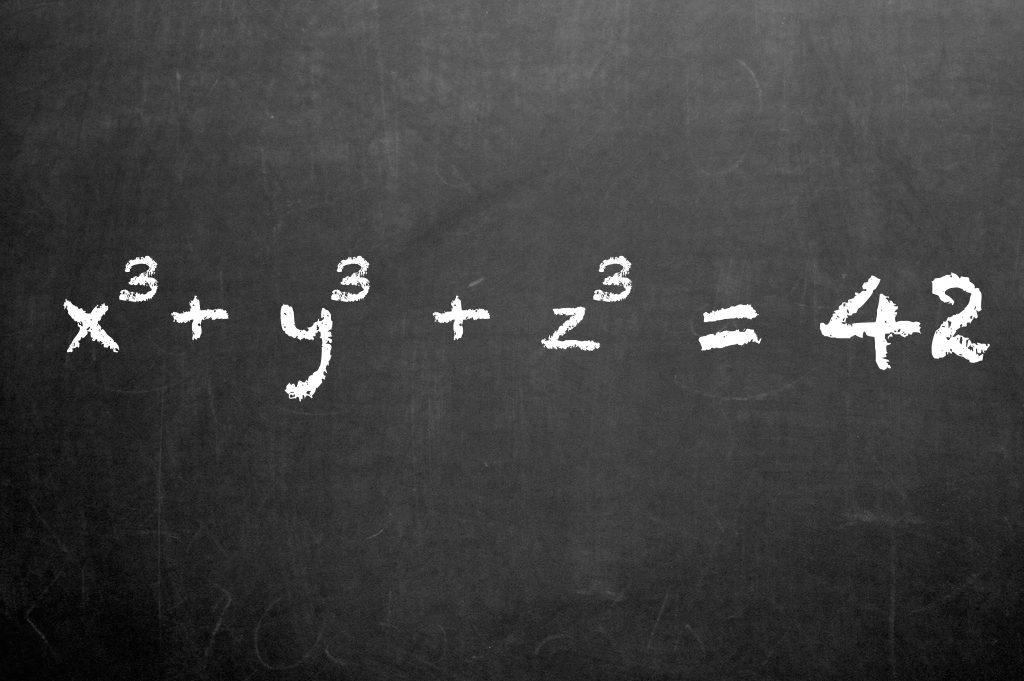
Uma equipa de cientistas da Universidade de Bristol e do Instituto Tecnológico de Massachusetts conseguiu finalmente resolver a última peça de um problema matemático com 65 anos.
O problema original, estabelecido em 1954 na Universidade de Cambridge, procurou soluções da equação diofantina x3 + y3 + z3 = k, com k sendo todos os números de 1 a 100.
x3 + y3 + z3 = k é a equação subjacente ao teimoso problema agora resolvido, uma equação diofantina, assim batizada em homenagem ao antigo matemático Diofante de Alexandria, que propôs um conjunto de equações semelhantes com múltiplas variáveis desconhecidas há cerca de 1.800 anos.
Esta equação funciona de uma forma muito simples: escolhemos qualquer número inteiro entre 1 e infinito e este passa a ser o nosso valor k. De seguida, o desafio é encontrar os valores para x, y e z que, quando divididos e somados, são iguais a k. Os números misteriosos podem ser positivos ou negativos, grandes ou pequenos. Se escolhermos, por exemplo, o número 8 e o fixarmos como valor k, uma possível solução para a equação seria: 23 + 13 + (-1)3 = 8.
Além das pequenas soluções facilmente encontradas, o problema tornou-se intratável, pois as respostas mais interessantes não conseguiam ser calculadas – tão numerosos foram os números necessários.
Porém, lentamente, ao longo de muitos anos, cada valor de k foi finalmente resolvido, graças a técnicas sofisticadas e computadores modernos – exceto os dois últimos, os mais difíceis de todos: 33 e 42. Em 2019, Andrew Booker encontrou uma resposta para 33, o que significa que só faltava resolver um último número pendente neste dilema de décadas, o mais difícil de quebrar.
No entanto, resolver o número 42 era ainda mais complexo do que o 33. Booker recorreu a Andrew Sutherland, recordista mundial com cálculos massivamente paralelos. Os dois investigadores chegaram à solução usando o Charity Engine: um “computador mundial” que aproveita o poder de computação ocioso e não utilizado de mais de 500 mil computadores domésticos para criar uma plataforma super-ecológica, feita inteiramente com capacidade desperdiçada.
A resposta, que levou mais de um milhão de horas de cálculo para provar, é a seguinte: X = -80538738812075974 Y = 80435758145817515 Z = 12602123297335631. Com estes números infinitamente improváveis, as famosas Soluções de Equação Diofantina (1954) podem finalmente descansar como todos os valores de k de 1 a 100 – até 42 – resolvidos.
“Sinto-me aliviado. Neste jogo, é impossível ter certeza de que encontraremos algo. É um pouco como tentar prever terremotos, pois temos apenas probabilidades aproximadas”, disse Booker em comunicado, citado pela Phys. “Portanto, podemos encontrar o que estamos à procura com alguns meses de pesquisa ou pode ser que a solução não seja encontrada durante mais um século.”
Além da equação diofantina agora desvendada, o mítico número 42 é também protagonista numa célebre história sobre o sentido da vida.
Na trilogia “The Hitchhiker’s Guide to the Galaxy”, escrita por Douglas Adams, um par de programadores encarrega o maior supercomputador da galáxia de responder à derradeira questão sobre a vida, universo e tudo mais. Após 7,5 milhões de anos a processar, o computador obtém uma resposta: 42.
Porém, depois desse tempo todo, já ninguém sabia qual tinha sido a questão colocada ao supercomputador – e muito menos o que a resposta significava na sua vida.
















O que não resolvem é o 44.
O rato esteve em Évora mas foi solto!
ahahha… BOA
Uma pergunta para os matemáticos que eventualmente leiam esta questão: Para que é que isto serve? Para que serve sabermos que, se X = -80538738812075974 Y = 80435758145817515 Z = 12602123297335631 então x3 + y3 + z3 = 42?
Qual foi a vantagem de todo o tempo perdido? Quero dizer, gasto? O que se ganhou com isso?
Leu o último parágrafo? De resto, é um jogo. Gosta de Sudoku? O que se ganha quando se resolve o jogo?
Ainda bem que o computador não respondeu 69…
Caro Fernando: para sua pergunta rasa, para dizer o mínimo, a resposta é profunda. Certamente a área aqui disponível não é suficiente. A matemática, com sua beleza muitas vezes incompreendida, não necessita de utilidade, imediata ou futura. Quantos teoremas, provas, conjecturas sobrevivem por anos sem solução ou aplicação para, um belo dia, figurar como resposta a uma pergunta prática, sua pricipal preocupação? Uma nova geometria foi necessária para atender as demandas da teoria da relatividade, de cujas consequências você certamente se beneficia todos os dias sem ter a menor ideia. Grande abraço de além mar!
quando divididos e somados?
Viva!
Dá para resolverem este meu problema que me subsiste há mais de uma década por favor:
x+y+z+w+k+(a+b) = números do próximo sorteio do euromilhões.
Muitíssimo agradecido 😉
Temerários …
Tentei, mas não deu 42, nem lá perto…
Mas tu és do norte…
https://defuse.ca/big-number-calculator.htm
resolveram até aparecer a próxima solução.
Sr Um Matematico, explica a um homem anonimo deste mundo como ele beneficia todos os dias da teoria da relatividade geral. E tambem se a matematica é uma matematica do Homem ou se existe a matematica em todo o universo. Ou seja, a matematica é uma linguagem do nosso universo só?
Boa noite a todos. Me chamo Odair José, sou professor de Matemática e um entusiasta da Teoria dos Números. Na verdade, essa é a minha linha de pesquisa a qual tenho me dedicado de forma muito enérgica há mais ou menos dez anos. A reação de um expectador ao tomar conhecimento de uma descoberta dessa magnitude depende essencialmente da sua formação acadêmica. Em outras palavras, não é de se esperar que indivíduos fora desse ambiente ou com uma formação distante das ciências exatas seja capaz de atribuir significado a descoberta em questão. Felizmente, existem muitos matemáticos profissionais que não pautam suas pesquisas nos aspectos práticos e/ou imediatos da sociedade. Alipas, graças a isso, eles são capazes de, muitas vezes, oferecer soluções quase que imediatas a problemas significativos da real, mesmo não tendo-os encarado diretamente. Particularmente, experimente a mesma alegria sempre que releio essa matéria assim como aconteceu na primeira vez. Considero até a possibilidade de apresentá-las aos meus alunos para que eles percebam os tipos de problemas que costumam despertar a atenção de grandes matemáticos e cientistas da computação em todo o mundo. No final da contas, a lição que fica é a seguinte: Havia uma pergunta extremamente interessante em aberto sobre uma das representações do número 42, tão simples de enunciar que qualquer estudante de nível médio é capaz de entender, mas incrivelmente difícil de responder. Porém, ainda assim, a questão foi resolvida e não é de surpreender que mais cedo ou mais tarde, alguém utilize essa informação em outros campos do conhecimento ou ainda para resolver outros problemas. Por último, fica a lição de que mesmo com toda a matemática produzida atualmente com destaque para a álgebra, os especialistas tiveram que recorrer aos supercomputadores, do contrário, não teriam tempo para processar todo esse volume de informações. Um abraço e espero que continuem divulgando o máximo de conhecimento matemático, independente do nível para que essa ciência se torna cada vez mais acessível de modo que qualquer pessoa seja capaz de perceber alguns traços da sua beleza.
(X=7 y=7 z=0)= 42 ñ pd ser assim?? Kjskjs