Adam Vaughan / EPA

Van Dijk, Gakpo e Konate a festejar o título da Premier League do Liverpool
A vitória do Liverpool FC no fim de semana garantiu-lhes o segundo título da Premier League, mas também resultou numa coisa curiosa – produziu uma série estranha de números nos livros de recordes da liga.
Acaba de acontecer algo de extraordinário no futebol inglês. O Liverpool sagrou-se campeão da Premier League pela segunda vez. A somar aos seus 18 títulos anteriores à Premier League, o clube iguala o recorde do Manchester United, que se sagrou campeão inglês por 20 vezes. Mas enquanto os adeptos do clube festejam sem dúvida este momento de triunfo, outra faceta espantosa do seu feito chamou a atenção dos matemáticos.
A conquista do título pelo Liverpool completou a abertura de um conjunto excecional de números que há 33 anos está a ser preparado. A sequência surge quando colocamos o Liverpool ao lado dos outros clubes que venceram a Premier League desde a sua criação, em 1992, listando-os pelo número de títulos conquistados, começando pelo mais baixo.
Como se pode ver na tabela abaixo, o número de títulos da Premier League é o seguinte: 1, 1, 2, 3, 5, 8, 13.
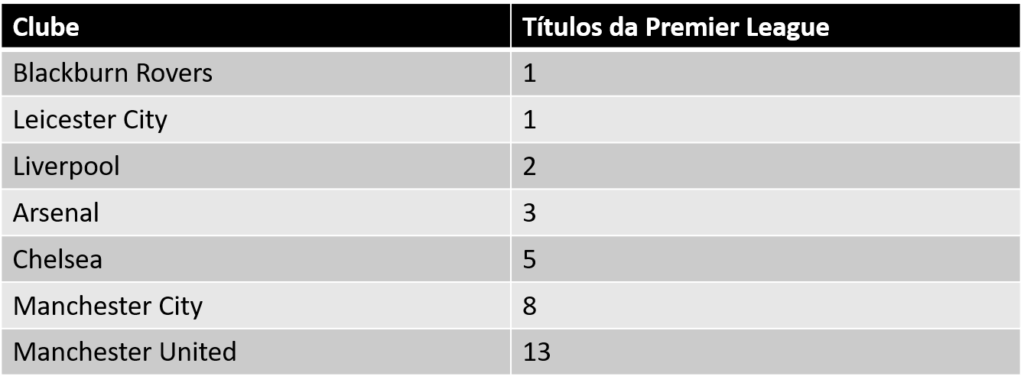
Para quem não sabe, esta sequência pode não parecer significativa. Mas será suficiente para entusiasmar muitos aficionados da matemática. Reconhecerão esta sequência como a sequência de Fibonacci, em que cada número (depois dos dois primeiros) é a soma dos dois anteriores da sequência.
A sequência pode ser encontrada numa variedade surpreendente de locais — desde as espirais das sementes nas cabeças dos girassóis e as brácteas das pinhas até aos padrões das árvores genealógicas de algumas espécies de animais.
As sequências de Fibonacci (sequências no plural, porque começar com um par diferente de números iniciais e seguir a regra de adicionar números consecutivos para gerar o seguinte dá-nos uma sequência diferente, mas relacionada) foram introduzidas pela primeira vez na ciência europeia em 1202 por Leonardo de Pisa, também conhecido pela sua alcunha Fibonacci (que significa filho de Bonaccio).
No entanto, muito antes de Fibonacci popularizar as sequências no seu livro Liber Abaci, as sequências já eram conhecidas dos matemáticos indianos. Estes tinham recorrido às sequências para os ajudar a enumerar o número de poemas possíveis de uma dada extensão, utilizando sílabas curtas de uma unidade de duração e sílabas longas de duas unidades de duração.
Os poetas/matemáticos indianos sabiam que se podia fazer um poema de comprimento n pegando num poema de comprimento n-1 e acrescentando-lhe uma sílaba curta ou num poema de comprimento n-2 e acrescentando-lhe uma sílaba longa. Consequentemente, descobriram que, para calcular o número de poemas de um determinado comprimento, bastava somar o número de poemas com uma sílaba a menos ao número de poemas com duas sílabas a menos – a regra exata que usamos hoje para definir uma sequência de Fibonacci.
Escondida nas sequências está outra importante e relacionada base matemática – a proporção áurea. À medida que os termos de uma sequência de Fibonacci aumentam, a razão entre cada termo e o anterior aproxima-se cada vez mais da razão áurea – aproximada a 1,61803 pelas primeiras casas na sua expansão decimal. Supõe-se que a proporção áurea governa a disposição das folhas no caule de algumas espécies de plantas e supostamente conduz a resultados esteticamente agradáveis quando aplicada na arte, arquitetura e música.
As sequências de Fibonacci são frequentemente consideradas pelos matemáticos como exemplos da beleza da matemática. Podem fornecer exemplos visuais vívidos da matemática inscrita nos padrões do mundo real, sem os quais muitos não matemáticos podem ter dificuldade em compreender a elegância que vemos na nossa disciplina.
No entanto, no nosso excesso de entusiasmo em fazer proselitismo, existe a tentação de apresentar as sequências de Fibonacci ou a proporção áurea como uma espécie de lei natural abrangente que rege fenómenos de várias ordens de grandeza, desde as formas espirais das conchas dos nautilus aos vórtices dos furacões e aos braços curvos das galáxias.
Na realidade, embora estas caraterísticas naturais sejam esteticamente agradáveis, muito poucas delas estão em conformidade com as regras da sequência de Fibonacci ou exibem a proporção áurea. Temos de ter cuidado para não tentarmos encaixar todos os belos padrões no delicado sapatinho de cristal de Fibonacci – para sugerirmos causalidade e impormos significado onde não existe.
Por vezes, as coincidências podem levar os cientistas ao erro, parecendo apontar para uma conclusão quando, na realidade, existe uma explicação alternativa para as observações que é melhor apoiada pelos factos.
O que significa, então, para o futebol, o facto de a bela e quase mística sequência de Fibonacci ter aparecido nos dados sobre o número de títulos conquistados na Premier League? Sem qualquer mecanismo plausível que possa ter dado origem à sequência, a resposta é quase de certeza nada.
É maravilhoso ter descoberto esta sequência matemática num local tão improvável, dando-nos a oportunidade de refletir sobre a importância dos números de Fibonacci. Mas um padrão nem sempre significa causalidade – uma coincidência é por vezes apenas uma coincidência.
ZAP // BBC