No final do século XIX, Karl Weierstrass inventou uma função que foi recebida como um “mal deplorável”. Com o tempo, aquela “função monstruosa” acabou por transformar os fundamentos da matemática.
Os seus conceitos fundamentais estavam enraizados na intuição e em argumentos informais, em vez de definições formais precisas. Até que, em resposta, surgiram duas escolas de pensamento.
Os matemáticos franceses estavam mais preocupados em aplicar o cálculo a problemas de física. Por outro lado, no século XIX, os matemáticos alemães começaram a deitar tudo o que se sabia abaixo. Começaram a procurar contra-exemplos que pudessem pôr em causa suposições há muito defendidas e acabaram por utilizar esses contra-exemplos para colocar o cálculo numa base mais estável e duradoura.
Um desses matemáticos foi Karl Weierstrass. Depois de ter desistido de estudar finanças, Weierstrass começou a carreira como matemático profissional quando tinha quase 40 anos.
No entanto, foi tempo suficiente para a revolucionar esta ciências, introduzindo um:
“Monstro Matemático”
Em 1872, Weierstrass publicou uma função que ameaçava tudo o que os matemáticos pensavam compreender sobre o cálculo.
Foi recebido com indiferença, raiva e medo, particularmente pelos gigantes matemáticos da escola de pensamento francesa.
Henri Poincaré, de um lado, nomeou a nova descoberta de Weierstrass como “um ultraje ao senso comum”.
Charles Hermite, por outro, chamou-lhe um “mal deplorável”.
Para perceber porque é que o resultado de Weierstrass foi tão mal recebido, a Quanta Magazine sugere que comecemos por compreender dois dos conceitos mais fundamentais do cálculo:
Continuidade
Uma função contínua é exatamente o que parece – uma função que não tem intervalos ou saltos. É possível traçar um caminho de qualquer ponto dessa função para qualquer outro sem levantar o lápis.
O cálculo consiste, em grande parte, em determinar a rapidez com que essas funções contínuas se alteram. Funciona, em termos gerais, aproximando uma dada função com linhas retas e não verticais.
Diferenciabilidade
Em qualquer ponto desta curva, é possível desenhar uma reta “tangente” – uma reta que melhor se aproxima da curva perto desse ponto. O declive, ou inclinação, da linha tangente mede a rapidez com que a função está a mudar nesse ponto. Pode definir outra função, chamada derivada, que fornece o declive da reta tangente em cada ponto da sua função original. Se a derivada existir em todos os pontos, diz-se que a função original é diferenciável.
As funções que contêm descontinuidades nunca são diferenciáveis.
Ou seja, não será possível desenhar uma reta tangente que se aproxime das descontinuidades, o que significa que a sua derivada não existirá aí. Mas mesmo as funções contínuas nem sempre são diferenciáveis em todos os pontos.
Este facto não incomodou a maioria dos matemáticos do século XIX. Viam-no como um fenómeno isolado. Desde que a função seja contínua, afirmavam, só pode haver um número finito de pontos onde a derivada não está definida. Em todos os outros pontos, a função deve continuar a ser agradável e suave. Por outras palavras, uma função só pode fazer ziguezagues e zagues até um certo ponto.
Ou talvez não…
De facto, em 1806, um proeminente matemático francês, André-Marie Ampère, afirmou que tinha provado este facto.
Durante décadas, o seu raciocínio não foi posto em causa… Até que surgiu o “Monstro de Weierstrass”.
Weierstrass descobriu uma função que, de acordo com a prova de Ampère, deveria ser impossível: Contínua em todo o lado e não diferenciável em lado nenhum. Construiu-a adicionando infinitamente muitas funções “cosseno” ondulatórias.
“Função patológica”? Custou a acreditar
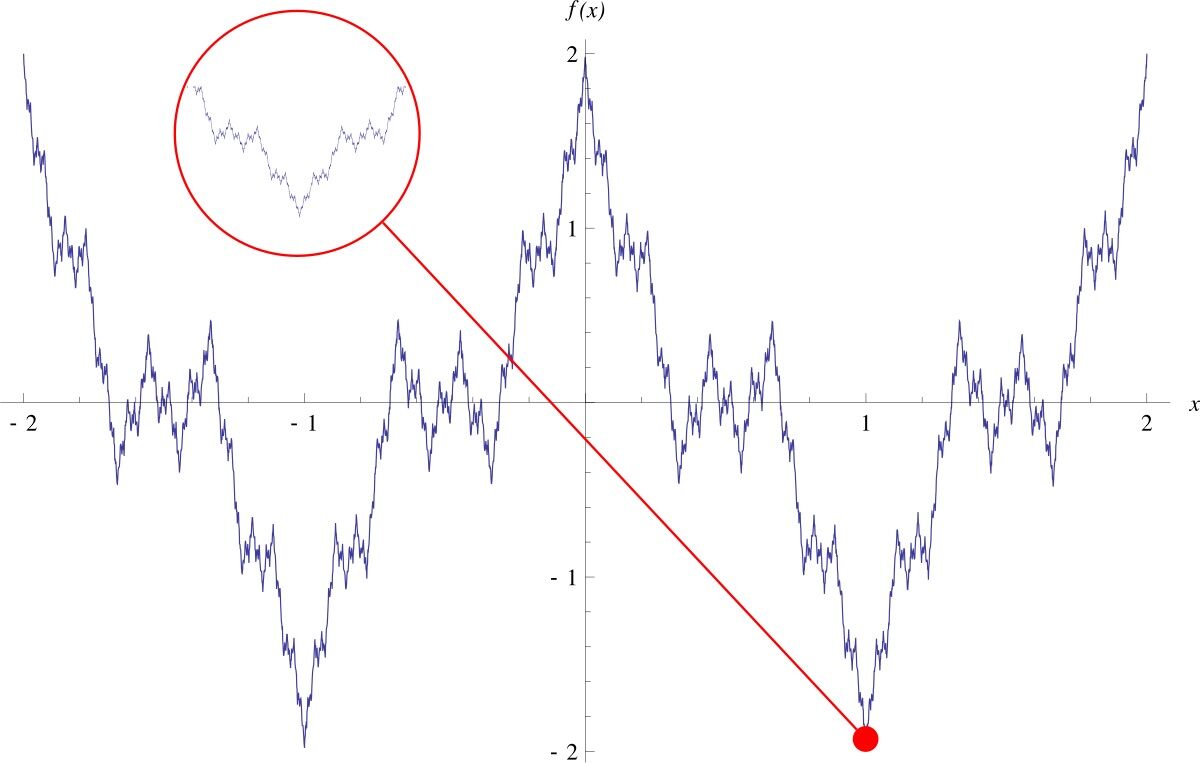
Muitos matemáticos rejeitaram a função. “Era uma anomalia”, diziam. Além disso, não conseguiam sequer visualizá-la. De facto, à primeira vista, quando se tenta traçar o gráfico da função de Weierstrass, parece contínuo em certas regiões.
Só com o zoom é que se vê que essas regiões também são “serrilhadas” e que vão continuar a ficar ainda mais serrilhadas e mal comportadas – aquilo a que os matemáticos chamam “patológico” – com cada ampliação adicional.
Mas Weierstrass tinha provado sem margem para dúvidas que, embora a sua função não tivesse descontinuidades, nunca era diferenciável.
Para o demonstrar, começou por rever as definições de “continuidade” e “diferenciabilidade” que tinham sido formuladas décadas antes pelos matemáticos Augustin-Louis Cauchy e Bernard Bolzano.
Como escreve a Quanta Magazine, estas definições baseavam-se em descrições vagas, em linguagem simples e numa notação inconsistente, o que as tornava fáceis de interpretar incorretamente. Por isso, Weierstrass reescreveu-as, utilizando uma linguagem precisa e fórmulas matemáticas concretas.
Com isso, conseguiu provar que, em cada ponto, a sua nova definição formal da derivada da função nunca tinha um valor finito; “rebentava” sempre até ao infinito.
Pelas palavras certas: a continuidade não implicava a diferenciabilidade.
E a sua função era mesmo monstruosa como os matemáticos tinham “receado”. Como “castigo”, foram obrigados a seguir as pisadas de Weierstrass.
Weierstrass revelou que a matemática está cheia de monstros: funções que parecem impossíveis, objetos estranhos, comportamentos selvagens,etc.; e a sua função acabou por ter muitas aplicações práticas.
No início do século XX, os físicos queriam estudar o movimento browniano, o movimento aleatório de partículas num líquido ou gás. Como este movimento é contínuo mas não suave – caracterizado por flutuações rápidas e infinitamente pequenas – funções como a de Weierstrass eram perfeitas para o modelar.
Da mesma forma, estas funções têm sido utilizadas para modelar a incerteza na forma como as pessoas tomam decisões e assumem riscos, bem como o comportamento dos mercados financeiros.