Um apocalipse zombie é sempre um problema difícil de resolver em todas as séries e filmes em que é retratado. No entanto, há uma fiel amiga que nos pode ajudar a escapar numa situação destas: a estatística.
Imagine que, ao acordar, ouvimos uma notícia urgente na rádio: “Foi lançado um vírus que transforma pessoas em zombies e é transmitido por uma mordida”. O que podemos fazer?
As opções são variadas. Podemos trancar-nos dentro de casa e torcer para que não sejamos infetados ou podemos fugir para longe, para algum abrigo onde ninguém nos encontre. Cada estratégia tem as suas vantagens e desvantagens, e muitos fatores determinam qual é a melhor.
Um zombie poderia partir a porta de sua casa? Será que vai correr o suficiente para chegar até ao esconderijo? Quantos zombies encontraremos no caminho para o abrigo? Quanto tempo levará para nos transformarmos se eles nos morderem? Existe uma cura?
O que existe é uma solução alternativa: usar a matemática e a estatística para escapar. Graças a elas, podemos modelar o comportamento da epidemia através do que é conhecido como modelos SIR.
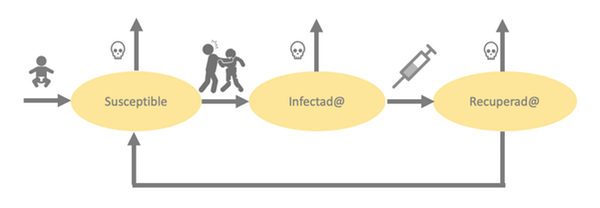
De um modo geral, um modelo SIR é um sistema de equações diferenciais que nos permite entender a dinâmica de uma infeção. Especificamente, como o número de pessoas suscetíveis a serem infetadas (S), o número de infetados (I) e o número de curados (R) variarão ao longo do tempo.
Para entender uma epidemia, precisamos de saber como é que ela é transmitida e quais variáveis a influenciam. Como é que se deixa de ser suscetível a ser infetado? E para ser curado? Pode tornar-se suscetível novamente após a recuperação?
Para responder a estas perguntas, precisamos de conhecer bem a epidemia. Felizmente para nós ainda não conhecemos os dados de uma infeção por zombies, mas esses modelos são úteis para entender muitas outras, como gripe, varicela e Ébola.
Na verdade, existem modelos matemáticos para entender quase todos os aspetos da vida. Modelos económicos, físicos, modelos climáticos, modelos biomédicos. Eles ajudam-nos a entender onde investir, como o coração bate e como escapar do fluxo piroclástico de um vulcão.
Mas (há sempre um mas) todos estes modelos sofrem o mesmo inconveniente. Eles são uma maneira de representar o nosso conhecimento sobre um fenómeno quase sempre incompleto. Isso deixa uma lacuna entre o modelo e a realidade que queremos explicar. Aqui entra a estatística.
As estatísticas estão por trás de cada novo tratamento médico, a eficácia de cada vacina, cada novo fertilizante. Também está por trás de muitas políticas ambientais, a recomendação de não fumar e que mulheres grávidas e crianças menores de 10 anos não consumam atum e espadarte. Por outras palavras, a estatística é a ciência que nos permite entender tudo o que o nosso conhecimento não alcança, quantificar a incerteza que nos cerca.
Voltemos ao caso dos modelos matemáticos. A metodologia estatística permite captar o que difere entre o processo real e o simulado e modelá-lo. Para entender melhor, pense numa reação química. Queremos saber com que rapidez é produzida e um especialista nos fornece uma fórmula que nos permite estimar essa velocidade a partir da quantidade de produto que não reagiu em todos os momentos. Então, repetimos a reação três vezes, medimos em vários instantes de tempo e obtemos uma aproximação ao valor desejado.
Até aqui tudo ótimo, mas na fórmula não foi tido em consideração que há sempre uma parte do produto que não reage, aderindo às paredes do recipiente. Tendo isto em conta, é muito possível que o valor da velocidade que estimamos esteja errado.
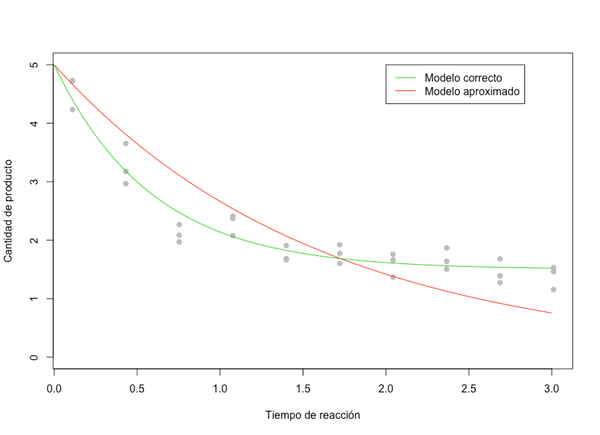
Podemos vê-lo no seguinte gráfico, onde os pontos representam a quantidade de produto que não reagiu a cada momento. A linha vermelha é o modelo errado, enquanto a verde representa o correto. A primeira estima que a taxa de reação é 0,63 quando, de facto, é 1,7.
O que fazemos então? Como poderíamos saber que o modelo estava errado? Na verdade, não podíamos, mas adicionamos uma correção estatística ao modelo, algo que só tem efeito quando o que observamos difere do modelo. Essa correção é conhecida como função de discrepância e, neste exemplo específico, permite recuperar uma estimativa do parâmetro em 1,72.
Tendo em mente que há incerteza, mesmo sobre o modelo que estamos a usar, é essencial para obter melhores resultados.
Mas como é que isso ajuda a escapar dos zombies? Bem, fácil: adicionar esta função de discrepância ao modelo SIR permite (se houver dados) estimar melhor a velocidade das criaturas, quanto tempo leva para ser infetado após a mordida e a eficácia da cura. Assim, as estatísticas ajudam-nos a decidir onde é melhor para se esconder.
ZAP // The Conversation