Manu Y
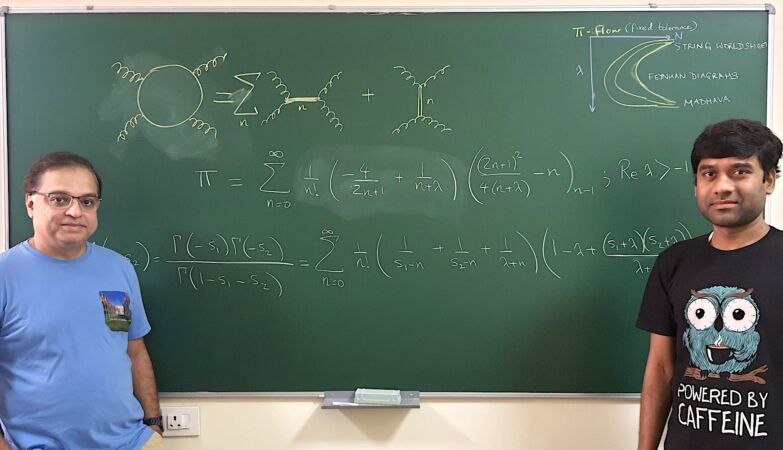
Aninda Sinha (esq) and Arnab Saha (dir)
Quando investigavam a forma como a Teoria das Cordas pode ser usada para explicar alguns fenómenos físicos, uma equipa de cientistas descobriu uma nova representação para o número pi.
Num novo estudo, publicado o mês passado na Physical Review Letters, os cientistas descobriram uma nova forma de representar pi, que combina parâmetros específicos de tal forma que podem ser incorporados em cálculos, como os usados para decifrar a dispersão de partículas de alta energia.
Até certo ponto, a nova fórmula está muito próxima da representação de pi sugerida pelo matemático indiano Sangamagrama Madhava no século XV, que foi a primeira série alguma vez registada do famoso pi, ou π — a razão entre o comprimento de uma circunferência e o seu diâmetro, cujo cálculo dá um número irracional que tende para 3,141592653……
Ou 3,14 para os amigos…
Segundo a Ciencia Plus, os investigadores não tinham o objetivo de encontrar essa fórmula no seu estudo, que se centrou inicialmente na análise da física de altas energias de modo a desenvolver um modelo com menos parâmetros para compreender como as partículas interagem.
“Inicialmente, os nossos esforços nunca foram no sentido de encontrar uma forma de olhar para o pi. Estávamos apenas a estudar a física de alta energia na teoria quântica e tentar desenvolver um modelo mais preciso para compreender como as partículas interagem”, afirma o professor e coautor do estudo, Aninda Sinha , em comunicado.
“Ficámos entusiasmados quando encontrámos uma nova forma de olhar para o pi”, acrescenta.
Para desenvolver um modelo eficiente, os cientistas combinaram duas ferramentas matemáticas, a função Euler-Beta e o diagrama de Feynman.
As funções Euler-Beta são funções matemáticas utilizadas para resolver problemas nas áreas da física e da engenharia, incluindo machine learning.
O diagrama de Feynman é uma representação matemática que explica a troca de energia que ocorre quando duas partículas interagem e se dispersam.
“Em matemática, uma série é usada para representar um parâmetro como pi na sua forma de componente. Se pi é o “prato”, então a série é a “receita” e pi pode ser representado como uma combinação de muitos números de parâmetros (ou ingredientes)”, realçam os cientistas.
Esta forma de representar interações complexas pertence à categoria de “problemas de otimização“, que proporcionam uma forma mais simples de extrair o valor de pi em cálculos envolvidos em processos de descodificação, como a dispersão quântica de partículas de alta energia.
“Os investigadores não o fizeram até agora porque não dispunham das ferramentas certas, que só foram descobertas através do trabalho que temos vindo a fazer com colaboradores nos últimos três anos”, explica Sinha.
“No início dos anos 70, os cientistas examinaram esta linha de investigação, mas rapidamente a abandonaram por ser demasiado complexa”.
Embora as descobertas ainda sejam muito superficiais, não é impossível que possam levar a aplicações práticas no futuro.