Na fronteira entre a Matemática e a Ciência da Computação, um matemático conseguiu resolver um problema de 30 anos.
Hao Huang, professor assistente de Matemática na Universidade Emory, em Atlanta, nos Estados Unidos, resolveu um problema de 30 anos, cruzando a área da Matemática com a da Ciência da Computação.
O professor provou a Conjetura da Sensibilidade, teoria que, de forma grosseira, afirma que podemos alterar o input para uma determinada função, sem alterar o output – a isto se chama de sensibilidade.
Segundo o Live Science, desde que os matemáticos propuseram esta teoria pela primeira vez, sem nunca a provar, os cientistas da computação perceberam que a Conjetura da Sensibilidade tem enormes implicações para determinar as formas mais eficientes de processar informação.
O mais impressionante não é o facto de Huang ter conseguido solucionar este problema, mas sim a forma elegante e direta como o fez, segundo especialistas da área. A sua solução ainda não passou a revisão por pares nem foi publicada numa revista científica, mas depois de a ter partilhado na Internet, os seus colegas rapidamente a aceitaram, dando-a como certa.
“Sempre que há algum anúncio deste género, 99% das vezes a solução está errada e é muito difícil que as pessoas de fora consigam avaliar. Este faz parte dos 1% dos casos. Estou muito confiante de que esta solução está correta. Porquê? Porque a li e entendi. Demorei cerca de meia hora”, escreveu no seu blogue Scott Aaronson, cientista de computação da Universidade do Texas, em Austin.
Ryan O’Donnell, professor de ciência da computação que estuda teoria dos números na Universidade Carnegie Mellon, em Pittsburgh, afirmou que a solução de Huang pode ser resumida num único tweet:
Mas, afinal, o que conseguiu provar Huang? Para simplificar, imagine um cubo 3D com lados com 1 unidade de comprimento. Se colocar este cubo num sistema de coordenadas 3D, um canto teria as coordenadas (0,0,0), o seguinte teria (1,0,0), o que se localiza acima dele seria (0,1,0), e assim sucessivamente.
Além disso, conseguimos retirar metade dos cantos (quatro) sem ter nenhum par de vizinhos: (0,0,0), (1,1,0), (1,0,1) e (0,1,1). Podemos comprová-lo observando o cubo, mas também o sabemos porque todos os lados são diferentes.
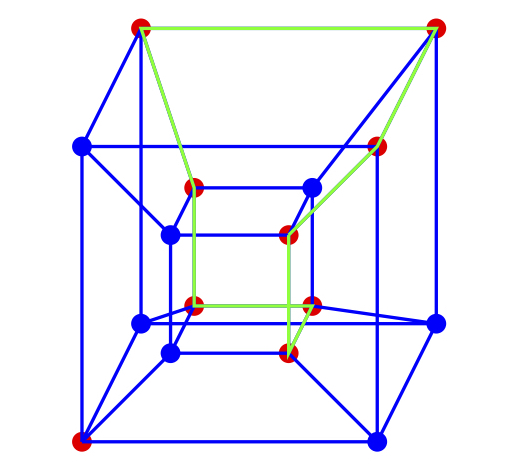
A Conjetura de Sensibilidade baseia-se em encontrar quantos vizinhos temos quando retiramos mais de metade dos vizinhos de um cubo de dimensão mais alta, ou hipercubo.
As coordenadas de um hipercubo são strings de 1s e 0s, onde o número de dimensões corresponde ao comprimento da string. Para um hipercubo 4D, por exemplo, existem 16 pontos diferentes, o que significa 16 strings diferentes de 1s e 0s com quatro dígitos.
Agora, escolha metade mais 1 pontos individuais no hipercubo – para um hipercubo 4D, isso significa escolher 9 ou 8 + 1 pontos diferentes de um total de 16.
A partir desse conjunto mais pequeno, encontre o ponto com o maior número de vizinhos. Os vizinhos diferem em apenas um número: por exemplo, 1111 e 1110 são vizinhos, porque só precisamos de trocar um dígito para transformar o primeiro no segundo.
Huang provou que este canto deve ter pelo menos tantos vizinhos quanto a raiz quadrada do número de dígitos – neste caso, a raiz quadrada de 4 – que é 2.
O matemático conseguiu chegar a esta conclusão conceptualizando o hipercubo usando matrizes de números em linhas e colunas, uma forma completamente inesperada de manipular uma matriz com um arranjo incomum de -1s e 1s. “Ele usou métodos espectrais, mas de uma maneira completamente nova. É muito misteriosa, mas prova que podemos usar esta técnica mais vezes”, escreveu um matemático.
A solução de Huang é empolgante porque dá mais um passo no campo da Ciência da Computação. No entanto, é também notória pelo facto de ter introduzido um novo método na Matemática.
ZAP // LiveScience / Quanta Magazine