dudeiwantthat.com

Formas 3D de largura constante. Aparentemente, também as há em dimensões superiores
Não satisfeitos com as já conhecidas formas em 2 ou 3 dimensões, os matemáticos descobriram agora “formas de largura constante” em qualquer número de dimensões espaciais — que rolam como uma roda apesar de não serem redondas.
Os matemáticos reinventaram a roda com a descoberta de formas que podem rolar suavemente quando colocadas entre duas superfícies — ou mesmo em quatro, cinco ou qualquer outro número superior de dimensões espaciais.
A descoberta responde a uma questão que os investigadores têm vindo a debater há décadas.
Estes objetos são conhecidos como formas de largura constante, e as mais familiares, em duas e três dimensões, são o círculo e a esfera. No entanto, estas não são as únicas formas deste género…
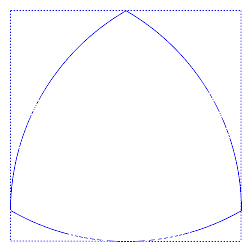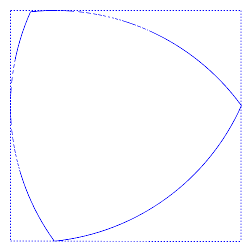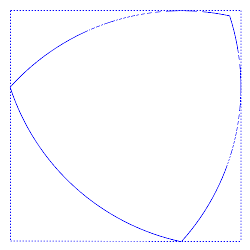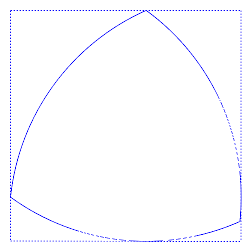
Um exemplo é o triângulo de Reuleaux, um triângulo com arestas curvas que é o exemplo mais simples dos chamados polígonos de Reuleaux, explica a New Scientist.
Outro exemplo conhecido (pelo menos, no Reino Unido) é a forma heptagonal com curvas equiláteras das moedas de 20 e 50 pence. Neste caso, o facto de terem uma largura constante permite-lhes rolar nas máquinas que funcionam com moedas e serem reconhecidas independentemente da sua orientação.
Fundamentalmente, estas formas têm uma área ou um volume mais pequeno do que um círculo ou uma esfera de largura equivalente (2 e 3 dimensões), mas, até agora, não se sabia se o mesmo poderia ser verdade em dimensões superiores.
Esta questão foi colocada pela primeira vez em 1988 pelo matemático israelo-americano Oded Schramm, que se interrogou se poderiam existir objetos de largura constante mais pequenos do que uma esfera de dimensão superior.
Embora as formas com mais de três dimensões sejam impossíveis de visualizar, os matemáticos podem defini-las alargando as formas 2D e 3D de forma lógica.
Por exemplo, tal como um círculo ou uma esfera é o conjunto de pontos que se situam a uma distância constante de um ponto central, o mesmo acontece em dimensões superiores.
“Por vezes, os fenómenos mais fascinantes são descobertos quando olhamos para dimensões cada vez mais elevadas”, diz Gil Kalai, investigador da Universidade Hebraica de Jerusalém, em Israel.
Agora, Andrii Arman, investigador da Universidade de Manitoba, no Canadá, e os seus colegas responderam à pergunta de Schramm e descobriram um conjunto de formas de largura constante, em qualquer dimensão, que são efetivamente mais pequenas do que uma esfera de dimensão equivalente.
Arman e os colegas trabalharam no problema durante anos, em reuniões semanais, tentando encontrar uma forma de construir estas formas antes de encontrarem uma solução. “Pode dizer-se que cansámos este problema até ele desistir“, afirma.
A primeira parte da prova consiste em considerar uma esfera com n dimensões e depois dividi-la em 2n partes iguais – ou seja, quatro partes para um círculo, oito para uma esfera 3D, 16 para uma esfera 4D e assim por diante.
Em seguida, os investigadores esticam e comprimem matematicamente estes segmentos para alterar a sua forma sem alterar a sua largura.
“A receita é muito simples, mas só o percebemos depois de toda a nossa elaboração”, diz Andriy Bondarenko, membro da equipa da Universidade Norueguesa de Ciência e Tecnologia.
A equipa provou que é sempre possível fazer esta distorção de modo a obter uma forma que tenha um volume no máximo 0,9n vezes superior ao da esfera de dimensão equivalente.
Isto significa que, à medida que se avança para dimensões cada vez maiores, a forma de largura constante torna-se proporcionalmente cada vez mais pequena em comparação com a esfera.
É difícil visualizar este fenómeno, mas um truque consiste em imaginar a silhueta a baixa dimensão de um objeto a alta dimensão. Quando vista de certos ângulos, a forma 3D aparece como um triângulo de Reuleaux 2D.
Andriy Prymak et al. 2024/SageMath/Danylo Radchenko

Uma forma 3D de largura constante vista de três ângulos diferentes. A vista do meio assemelha-se a um triângulo de Reuleaux 2D
Da mesma forma, a forma 3D pode ser vista como uma “sombra” da forma 4D, e assim por diante. “As formas em dimensões superiores serão, em certo sentido, semelhantes, mas aumentarão de complexidade à medida que a dimensão aumenta”, diz Arman.
Tendo identificado estas formas, os matemáticos esperam agora estudá-las mais aprofundadamente. “Mesmo com o novo resultado, que elimina algum do mistério sobre elas, são conjuntos muito misteriosos em dimensões elevadas“, diz Kalai.