ZAP // geralt / Pixabay

A probabilidade de acertar nos 6 números da lotaria é muito, muito baixa. Mas a probabilidade de os mesmos 6 números saírem duas vezes é muito mais alta do que se possa pensar.
A 10 de setembro de 2009, a lotaria nacional búlgara anunciou que os números vencedores dessa semana eram 4, 15, 23, 24, 35 e 42.
Este é um conjunto de números perfeitamente normal, poderíamos pensar — a não ser que tivéssemos visto o sorteio apenas quatro dias antes, no qual tinha saído exatamente a mesma combinação.
“Não se pode dizer que isto seja um jogo de azar!”, pode estar a pensar — e não seria há única pessoa. “Aqui há gato“, pensaram na altura milhares de búlgaros.
As pessoas exigiram uma investigação; foi aberto um inquérito governamental para excluir a possibilidade de fraude ou manipulação — mas nunca foi detetada qualquer irregularidade.
E isso… faz todo o sentido, na verdade: acontece que a probabilidade de acontecerem coincidências estranhas é muito maior do que se possa pensar, explica o IFLS.
A ideia de um resultado de um em catorze milhões aparecer duas vezes no espaço de quatro dias pode ser um pouco confusa, por isso vamos começar com um exemplo mais simples.
Qual é a dimensão mínima que um grupo de pessoas tem que ter para que haja uma probabilidade maior do que 50% de que duas delas partilhem a mesma data de aniversário?
A resposta surpreendente é apenas 23, ou seja, se tomarmos um qualquer número de 23 pessoas, há uma probabilidade de mais de 50% de que duas quaisquer delas soprem as velas no mesmo dia.
Talvez já tenha ouvido este problema antes — é bastante famoso. É conhecido como o “paradoxo do aniversário“, embora não tenha nada de paradoxal: é apenas inesperado que o resultado seja um número tão baixo.
Num grupo de apenas duas pessoas, a probabilidade de não partilharem a mesma data de aniversário é muito elevada: 99,7%. Ora, se houver três pessoas nesse grupo, a probabilidade de os aniversários não coincidirem já baixa para 99,2 %.
Quanto mais pessoas se acrescentar ao grupo, menor é a percentagem. Contudo, não é preciso ter 183 pessoas para chegar aos 50%: quando se chega a apenas 23 pessoas, a probabilidade acima cai para 49,3%.
Mas se partilhar o seu local de trabalho com 41 pessoas, por exemplo, a sua probabilidade de partilhar um aniversário com um colega já aumenta mais mais de 90%. Com 60 pessoas, é superior a 99%. E com 100, a probabilidade de duas pessoas do grupo terem a mesma data de aniversário é de 99,99997%.
Duas vezes na vida
Agora que já sabemos de onde vêm estas probabilidades mais baixas do que o esperado, como é que explicamos os sorteios idênticos da lotaria?
Primeiro, vamos rever o sistema: a lotaria búlgara usa uma seleção aleatória de seis números de um conjunto de 49.
Na altura, os responsáveis pela lotaria afirmaram que era impossível adulterar as máquinas; os sorteios “têm lugar na presença de um comité especial e são transmitidos em direto na televisão nacional, o que garante que não há batota“, disseram à Reuters na altura.
Isso faz com que qualquer conjunto de seis números tenha uma ocorrência de apenas 1 em 13.983.816:, o resultado de um cálculo combinatório pronunciado como “49 escolhe 6” — ou “combinação de sessenta elementos tomados seis a seis” e representado pela fórmula abaixo:
ZAP
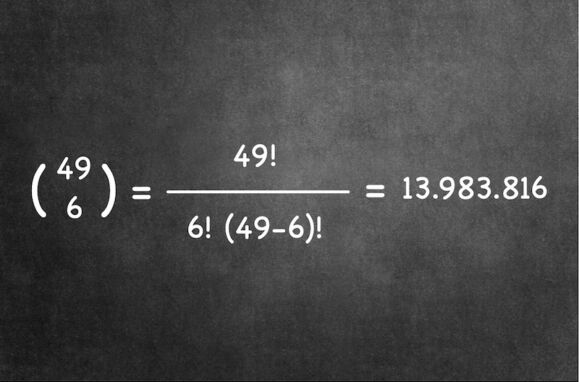
Não, não estamos super-excitados com a fórmula! O “!” significa “fatorial”. Ou seja, a combinação de 60 elementos tomados 6 a 6 é igual ao fatorial de 49 sobre a multiplicação do fatorial de 6 pela diferença entre o fatorial de 49 e o fatorial de 6. Há quem diga que é simples…
Portanto, sim, as hipóteses de a combinação exacta que saiu na Bulgária a 6 de setembro voltar a ocorrer seriam, para dizer o mínimo, extremamente improváveis. Mas, tal como no caso do paradoxo do aniversário, não é essa a pergunta que deveríamos estar a fazer.
“A probabilidade de dois sorteios em particular coincidirem é de uma em 13.983.816”, explica David Hand, professor de Matemática do Imperial College London, num artigo na Scientific American.
“Mas qual é a probabilidade de quaisquer dois sorteios entre três sorteios coincidirem? Ou a hipótese de alguns dois sorteios entre 50 sorteios coincidirem?”, questiona o investigador.
Afinal de contas, explica Hand, em quaisquer três sorteios da lotaria, há três formas potenciais de dois deles coincidirem. Em quatro sorteios, há seis pares possíveis; em cinco sorteios, há dez. Quando se chega aos 50 sorteios, há 1.225 pares possíveis, e com 1.000 sorteios, há 499.500 maneiras possíveis de dois conjuntos de números coincidirem.
Isto aumenta drasticamente as probabilidades. Quando tiver feito 4.404 sorteios, é mais provável do que nunca que dois sorteios coincidam exatamente — e como Hand salienta, “se ocorrerem dois sorteios por semana, perfazendo 104 num ano, este número de sorteios demorará menos de 43 anos“.
Afinal, não é assim tão surpreendente que tenha acontecido uma vez há 15 anos — ou, de facto, que também tenha acontecido noutras ocasiões. “Quando temos em conta o número de lotarias em todo o mundo, vemos que seria espantoso se os sorteios não se repetissem ocasionalmente”, observou Hand.
É claro que quatro dias é muito menos do que 43 anos — mas é evidente que a duplicação nunca foi tão estranha como parecia à primeira vista. De facto, no fim de contas, foi um evento particularmente azarado: “Ninguém ganhou o prémio principal no primeiro sorteio”, informou a BBC na altura.
Mas um recorde de 18 pessoas adivinhou os seis números no sorteio de 10 de setembro. Aparentemente, há muito mais pessoas a acreditar em milagres — e em coincidências estranhas — do que poderíamos pensar.














Mentira